题目内容
【题目】某学习小组在学习了函数及函数图象的知识后,想利用此知识来探究周长一定的矩形其边长分别为多少时面积最大. 请将他们的探究过程补充完整.
(1)列函数表达式:若矩形的周长为8,设矩形的一边长为x,面积为y,则有y=____________;
(2)上述函数表达式中,自变量x的取值范围是____________;
(3)列表:
x | … | 0.5 | 1 | 1.5 | 2 | 2.5 | 3 | 3.5 | … |
y | … | 1.75 | 3 | 3.75 | 4 | 3.75 | 3 | m | … |
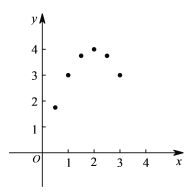
写出m=____________;
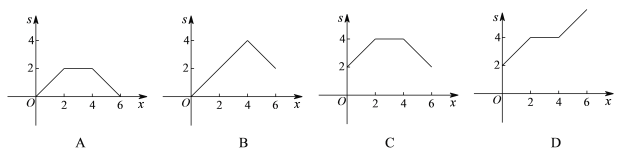
(4)画图:在平面直角坐标系中已描出了上表中部分各对应值为坐标的点,请你画出该函数的图象;
(5)结合图象可得,x=____________时,矩形的面积最大;写出该函数的其它性质(一条即可):____________.
【答案】见解析
【解析】
(1)根据矩形的周长表示出另一边长,然后利用矩形面积公式即可求得y与x间的关系式;
(2)根据矩形周长以及边长大于0即可求得;
(3)把x=3.5代入(1)中的解析式即可求得m的值;
(4)按从左到右的顺序用平滑的曲线进行画图即可;
(5)观察图象即可得.
(1)因为矩形一边长为x,则另一边长为(![]() -x)=(4-x),
-x)=(4-x),
依题意得:矩形的面积y=x(4-x),
即y=-x2+4x,
故答案为:-x2 + 4x;
(2)由题意得![]() ,解得:0<x<4,
,解得:0<x<4,
故答案为:0<x<4;
(3)当x=3.5时,y=-3.52+4×3.5=1.75,
故答案为:1.75;
(4)如图所示;
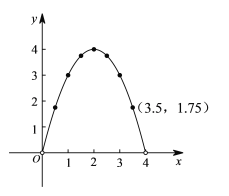
(5)观察图象可知当x=2时矩形面积最大,
轴对称图形;当0<x≤2时,y随x的增大而增大等,
故答案为:2;轴对称图形或当0<x≤2时,y随x的增大而增大.

【题目】从2013年1月7日起,中国中东部大部分地区持续出现雾霾天气.某市记者为了了解”雾霾天气的主要原因“,随机调查了该市部分市民,并对调查结果进行整理.绘制了如下尚不完整的统计图表.
组别 | 观点 | 频数(人数) |
A | 大气气压低,空气不流动 | 80 |
B | 地面灰尘大,空气湿度低 | m |
C | 汽车尾气排放 | n |
D | 工厂造成的污染 | 120 |
E | 其他 | 60 |
请根据图表中提供的信息解答下列问题: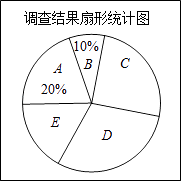
(1)填空:m= , n= . 扇形统计图中E组所占的百分比为%;
(2)若该市人口约有100万人,请你估计其中持D组“观点”的市民人数;
(3)若在这次接受调查的市民中,随机抽查一人,则此人持C组“观点”的概率是多少?