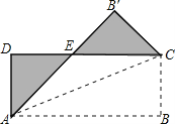
题目内容
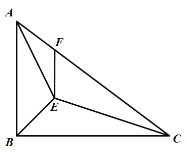
【题目】如图,在等腰![]() 中,
中,![]() ,
,![]() ,
,![]() 是
是![]() 边上的中点,点
边上的中点,点![]() 、
、![]() 分别在
分别在![]() 、
、![]() 边上运动,且保持
边上运动,且保持![]() ,连接
,连接![]() 、
、![]() 、
、![]() .在此运动变化的过程中,下列结论:①
.在此运动变化的过程中,下列结论:①![]() 是等腰直角三角形;②四边形
是等腰直角三角形;②四边形![]() 不可能为正方形;③
不可能为正方形;③![]() ;④四边形
;④四边形![]() 的面积保持不变;⑤
的面积保持不变;⑤![]() 面积最大值为8,其中正确的结论是___________(填番号).
面积最大值为8,其中正确的结论是___________(填番号).
【答案】①③④⑤
【解析】
连接CF,由SAS定理可得△CFE≌△ADF,从而可证∠DFE=90°可得DF=EF,可得①△DFE是等腰直角三角形正确;显而易见③正确,再由补割法可证④是正确的.判断②与⑤,当DF⊥BC时,DF最小,DF取最小值4,△CDE最大的面积等于四边形CDEF的面积减去△DEF的最小面积,此时四边形CDFE是正方形,由此可知⑤是正确的,②错误;故①③④⑤正确.
解:连接CF,
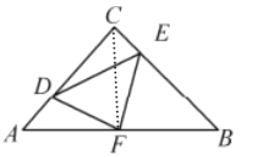
∵△ABC为等腰直角三角形,![]() 是
是![]() 边上的中点,
边上的中点,
∴∠FCB=∠A=45°, CF=AF=FB,
∵AD=CE
∴△ADF≌△CEF
∴EF=DF , ∠CFE=∠AFD
∵∠AFD+∠CFD=90°
∴∠CFE+∠CFD=∠EFD=90°
∴△EDF是等腰直角三角形,
所以①正确;
当D、E分别为AC、BC的中点时,DF∥BC,EF∥CD
∴四边形CDEF是平行四边形,
又∵DF=EF
∴四边形CDEF是正方形,
因此②错误;
在等腰![]() 中,
中,![]()
∴AC=BC
∵AD=CE, CD=AC-AD,EB=BC-CE,
∴CD=EB
③是正确的;
由△ADF≌△CEF可知S△ADF=S△CEF
S四边形CDFE=S△CDF+S△CEF= S△CDF+S△ADF
=S△ACF=![]() S△ABC=
S△ABC=![]() ×
×![]() ×8×8=16
×8×8=16
即四边形CDFE的面积保持不变.
由此④正确;
∵△DEF是等腰直角三角形,
当DE最小时,DF也最小,
即当DF⊥AC时,DE最小,
此时DF∥CB,DF=![]() BC
BC
当△CDE面积最大时,△DEF的面积最小,
此时,
S△CDE=S四边形CEFD-S△DEF
=16-![]() DF·EF
DF·EF
=16-![]() ×4×4
×4×4
=8,
所以⑤正确.
综上所述正确的有①③④⑤.
故答案为:①③④⑤

 名校课堂系列答案
名校课堂系列答案【题目】八(2)班分成甲、乙两组进行一分钟投篮测试,并规定得6分及以上为合格,得9分及以上为优秀,现两组学生的一次测试成绩统计如下表:
成绩(分) | 4 | 5 | 6 | 7 | 8 | 9 |
甲组人数(人) | 1 | 2 | 5 | 2 | 1 | 4 |
乙组人数(人) | 1 | 1 | 4 | 5 | 2 | 2 |
(1)请你根据上表数据,把下面的统计表补充完整,并写出求甲组平均分的过程;
统计量 | 平均分 | 方差 | 众数 | 中位数 | 合格率 | 优秀率 |
甲组 |
| 2.56 |
| 6 | 80.0% | 26.7% |
乙组 | 6.8 | 1.76 | 7 |
| 86.7% | 13.3% |
(2)如果从投篮的稳定性角度进行评价,你认为哪组成绩更好?并说明理由;
(3)小聪认为甲组成绩好于乙组,请你说出支持小聪观点的理由;