题目内容
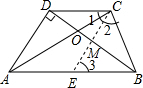
如图所示，梯形ABCD中，AB∥CD，两对角线AC、BD交于0点，且BD⊥AD，已知BC=CD=7，则AB=______．
过C作CE∥AD，
∵DC∥AB，
∴四边形ADCE是平行四边形，
∴AE=DC=7，
∵BD⊥AD，
∴∠ADB=90°，
∵AD∥BC，
∴∠EMB=∠ADB=90°，
∴CM⊥DB，
∵DC=BC，
∴△DCB是等腰三角形，
∴∠1=∠2，
∵DC∥AB，
∴∠1=∠3，
∴∠2=∠3，
∴EB=CB=7，
∴AB=7+7=14，
故答案为：14．
∵DC∥AB，
∴四边形ADCE是平行四边形，
∴AE=DC=7，
∵BD⊥AD，
∴∠ADB=90°，
∵AD∥BC，
∴∠EMB=∠ADB=90°，
∴CM⊥DB，
∵DC=BC，
∴△DCB是等腰三角形，
∴∠1=∠2，
∵DC∥AB，
∴∠1=∠3，
∴∠2=∠3，
∴EB=CB=7，
∴AB=7+7=14，
故答案为：14．
练习册系列答案
相关题目
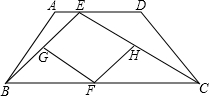别是BE、BC、CE的中点．