题目内容
发射一枚炮弹,经过x秒后炮弹的高度为y米,x,y满足y=ax2+bx,其中a,b是常数,且a≠0.若此炮弹在第6秒与第14秒时的高度相等,则炮弹达到最大高度的时刻是( )
| A.第8秒 | B.第10秒 | C.第12秒 | D.第15秒 |
B
解析试题分析:由于炮弹在第6s与第14s时的高度相等,即x取6和14时y的值相等,根据抛物线的对称性可得到抛物线y=ax2+bx的对称轴为直线x="6+" 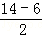 =10,然后根据二次函数的最大值问题求解.
=10,然后根据二次函数的最大值问题求解.
∵x取6和14时y的值相等,
∴抛物线y=ax2+bx的对称轴为直线x=6+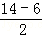 =10,
=10,
即炮弹达到最大高度的时间是10s.
故选:B.
考点:二次函数的应用.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
为提醒人们节约用水,及时修好漏水的水龙头.两名同学分别做了水龙头漏水实验,他们用于接水的量筒最大容量为100毫升.
实验一:小王同学在做水龙头漏水实验时,每隔10秒观察量筒中水的体积,记录的数据如表(漏出的水量精确到1毫升):
| 时间t(秒) | 10 | 20 | 30 | 40 | 50 | 60 | 70 |
| 漏出的水量V(毫升) | 2 | 5 | 8 | 11 | 14 | 17 | 20 |

(2)如果小王同学继续实验,请探求多少秒后量筒中的水会满而溢出(精确到1秒)?
(3)按此漏水速度,一小时会漏水 千克(精确到0.1千克)
实验二:
小李同学根据自己的实验数据画出的图象如图2所示,为什么图象中会出现与横轴“平行”的部分?

已知二次函数y=ax2+bx+c的图象如图,①abc>0;②b<a+c;③4a+2b+c>0;④2c<3b;⑤a+b>m(am+b)(m≠1),其中结论正确的有( )
| A.③④ | B.③⑤ | C.③④⑤ | D.②③④⑤ |
在平面直角坐标系中,将抛物线y=3x2先向右平移1个单位,再向上平移2个单位,得到的抛物线的解析式是( )
| A.y=3(x+1)2+2 | B.y=3(x+1)2﹣2 |
| C.y=3(x﹣1)2+2 | D.y=3(x﹣1)2﹣2 |
已知抛物线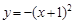 上的两点
上的两点 ,如果
,如果 ,那么下列结论一定成立的是
,那么下列结论一定成立的是
A. | B. | C. | D. . . |
已知:M、N两点关于y轴对称,且点M在双曲线 上,点N在直线
上,点N在直线 上,设点M的坐标为
上,设点M的坐标为 ,则二次函数
,则二次函数 ( )
( )
A.有最大值,最大值为 | B.有最大值,最大值为 |
C.有最小值,最小值为 | D.有最小值,最小值为 |
 与
与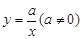 在同一直角坐标系中的图象可能是( )
在同一直角坐标系中的图象可能是( )