��Ŀ����
Ϊ�������ǽ�Լ��ˮ����ʱ��©ˮ��ˮ��ͷ������ͬѧ�ֱ�����ˮ��ͷ©ˮʵ�飬�������ڽ�ˮ����Ͳ�������Ϊ100������
ʵ��һ��С��ͬѧ����ˮ��ͷ©ˮʵ��ʱ��ÿ��10��۲���Ͳ��ˮ���������¼�����������©����ˮ����ȷ��1��������
| ʱ��t���룩 | 10 | 20 | 30 | 40 | 50 | 60 | 70 |
| ©����ˮ��V�������� | 2 | 5 | 8 | 11 | 14 | 17 | 20 |

��2�����С��ͬѧ����ʵ�飬��̽����������Ͳ�е�ˮ�������������ȷ��1�룩��
��3������©ˮ�ٶȣ�һСʱ��©ˮ��������ǧ�ˣ���ȷ��0.1ǧ�ˣ�
ʵ�����
С��ͬѧ�����Լ���ʵ�����ݻ�����ͼ����ͼ2��ʾ��Ϊʲôͼ���л��������ᡰƽ�С��IJ��֣�

ʵ��һ����1����ͼ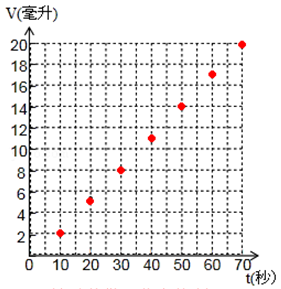
��2��337�� ��3��1.1ǧ��
ʵ�����������
�������������ʵ��һ��
��1������ͼ�е�����ֱ��������ϵ��������㼴�ɡ�
��2�������V��t�ĺ�����ϵʽΪV=kt+b�����ݱ������ݣ��ó�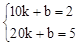 �����V��t�ĺ�����ϵʽ���ٸ���
�����V��t�ĺ�����ϵʽ���ٸ���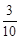 t��1��100����Ͳ������������������������Ͳ�е�ˮ�����濪ʼ�����
t��1��100����Ͳ������������������������Ͳ�е�ˮ�����濪ʼ�����
��3�����ݣ�2���еĺ�����ϵʽ����t=3600����뼴������𰸣�һСʱ��©ˮ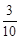 ��3600��1=1079��������=1079���ˣ���1.1ǧ�ˡ�
��3600��1=1079��������=1079���ˣ���1.1ǧ�ˡ�
ʵ���������С��ͬѧ��ˮ����Ͳװ����ʼ�������Ͳ�ڵ�ˮ���ٷ����仯�����ɵó�ͼ���л��������ᡰƽ�С��IJ��֡���
�⣺ʵ��һ��
�������� ��1����ͼ����ͼ��ʾ��
��2���ɣ�1������V��t�ĺ�����ϵʽΪV=kt+b��
�����ݱ�������֪����t=10ʱ��V=2����t=20ʱ��V=5��
��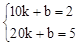 ����ã�
����ã�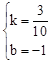 ��
��
�ྭ��֤��V��t�ĺ�����ϵʽΪV=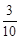 t��1��
t��1��
������ã�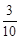 t��1��100�����t��
t��1��100�����t��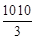 =336
=336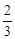 ��
��
��337�����Ͳ�е�ˮ�����濪ʼ�����
��3��1.1��
ʵ�����
��С��ͬѧ��ˮ����Ͳװ����ʼ�������Ͳ�ڵ�ˮλ���ٷ����仯��
��ͼ���л��������ᡰƽ�С��IJ��֡�

ij�̳��ƻ�����A��B�������ͽ���̨�ƹ�100յ��������̨�ƵĽ��ۡ��ۼ������ʾ��
| ���� �۸� | ���ۣ�Ԫ/յ�� | �ۼۣ�Ԫ/յ�� |
| A�� | 30 | 45 |
| B�� | 50 | 70 |
��2�����̳��涨B��̨�ƵĽ�������������A��̨��������3����Ӧ������������ʹ�̳�������������̨��ʱ������ࣿ��ʱ����Ϊ����Ԫ��
����һö�ڵ�������x����ڵ��ĸ߶�Ϊy�ף�x��y����y=ax2+bx������a��b�dz�������a��0�������ڵ��ڵ�6�����14��ʱ�ĸ߶���ȣ����ڵ��ﵽ���߶ȵ�ʱ���ǣ�������
| A����8�� | B����10�� | C����12�� | D����15�� |
��������y=��x-1��2+3����ƽ��1����λ��������ƽ��3����λ�����������ߵĽ���ʽΪ��������
| A��y=��x-2��2 | B��y=��x-2��2+6 | C��y=x2+6 | D��y=x2 |





