题目内容
如图,在矩形ABCD中,AB=9,BC=3,点E是沿A→B方向运动,点F是沿A→D→C方向运动.现E、F两点同时出发匀速运动,设点E的运动速度为每秒1个单位长度,点F的运动速度为每秒3个单位长度,当点F运动到C点时,点E立即停止运动.连接EF,设点E的运动时间为x秒,EF的长度为y个单位长度,则下列图象中,能表示y与x的函数关系的图象大致是( )
A. | B. | C. | D. |
C.
解析试题分析:分两种情况讨论:
①当点E是沿A→B方向运动,点F是沿A→D方向运动时,此时, ,AE=x,AF=3x,
,AE=x,AF=3x,
∴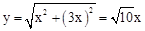 .
.
②当点E是沿A→B方向运动,点F是沿D→C方向运动时,如答图,过点F作FH⊥AB于点H, ,AH=
,AH= , HE=
, HE= ,
,
∴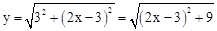 .
.
∵ ,
,
∴当 时,
时, 有最小值,即y有最小值.
有最小值,即y有最小值.
故选C.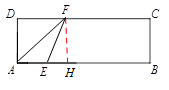
考点:1.双动点问题的函数图象;2.勾股定理;3.分类思想的应用.

练习册系列答案
 芝麻开花课程新体验系列答案
芝麻开花课程新体验系列答案
相关题目
发射一枚炮弹,经过x秒后炮弹的高度为y米,x,y满足y=ax2+bx,其中a,b是常数,且a≠0.若此炮弹在第6秒与第14秒时的高度相等,则炮弹达到最大高度的时刻是( )
| A.第8秒 | B.第10秒 | C.第12秒 | D.第15秒 |
二次函数y=ax2+bx+c(a≠0)的图象如图所示,若|ax2+bx+c|=k(k≠0)有两个不相等的实数根,则k的取值范围是( )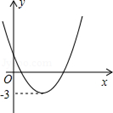
| A.k<-3 | B.k>-3 | C.k<3 | D.k>3 |
已知二次函数 的图象与x轴的一个交点为(1,0),则它与x轴的另一个交点坐标是
的图象与x轴的一个交点为(1,0),则它与x轴的另一个交点坐标是
| A.(1,0) | B.(-1,0) | C.(2,0) | D.(-2,0) |
二次函数y=x2的图象向上平移2个单位,得到新的图象的二次函数表达式是( )
A. | B. | C. | D. |
将抛物线y=(x-1)2+3向左平移1个单位,再向下平移3个单位后所得抛物线的解析式为( )
| A.y=(x-2)2 | B.y=(x-2)2+6 | C.y=x2+6 | D.y=x2 |
二次函数y=ax2+bx+c(a≠0)的图象如图所示,则下列结论中,正确的是( )
| A.abc<0 |
| B.a+c<b |
| C.b>2a |
| D.4a>2b﹣c |


