��Ŀ����
����Ŀ��(1)����
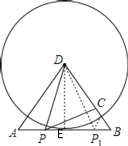
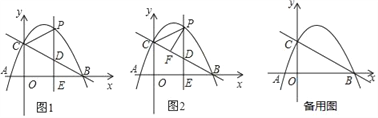
��ͼ1�����ı���ABCD�У���PΪAB��һ�㣬��DPC=��A=��B=90������֤��ADBC=APBP.
(2)̽��
��ͼ2�����ı���ABCD�У���PΪAB��һ�㣬��DPC=��A=��B=��ʱ�����������Ƿ���Ȼ������˵������.
(3)Ӧ��
������(1)(2)��õľ��������⣺��ͼ3������ABD�У�AB=6��AD=BD=5����P��ÿ��1����λ���ȵ��ٶȣ��ɵ�A�������ر�AB���B�˶�����������DPC=��A�����P���˶�ʱ��Ϊt(��)������DΪԲ�ģ���DCΪ�뾶��Բ��AB����ʱ����t��ֵ.
���𰸡�(1)֤����������(2)����ADBC=APBP�Գ��������ɼ�������(3)t��ֵΪ2���10�룮
��������
��1������ͬ�ǵ������ȣ�����֤����APD=��BPC��Ȼ��������������ε��ж�����֤������ADP�ס�BPC���ٸ������������ε����ʣ��г�����ʽ�������ݱ����Ļ������ʼ���֤�����ۣ�
��2��������������ǵ����ʺ���֪����֤������BPC=��APD��Ȼ��������������ε��ж�����֤������ADP�ס�BPC���ٸ������������ε����ʣ��г�����ʽ�������ݱ����Ļ������ʼ���֤�����ۣ�
��3������D��DE��AB�ڵ�E���������ߺ�һ���ɶ������DE��Ȼ��Բ�������ߵ����ʿɵã�DC=DE=8���ٸ���(1)(2)�ľ����ADBC=APBP���г����̣����t��ֵ����.
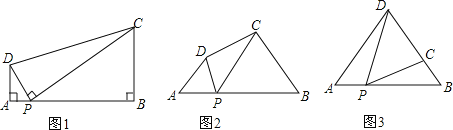
(1)֤�����ߡ�DPC=��A=��B=90�㣬
���ADP+��APD=90�㣬��BPC+��APD=90�㣬
���APD=��BPC��
���ADP�ס�BPC��
��![]()
��ADBC=APBP��
(2)����ADBC=APBP�Գ��������ɣ�
֤�����ߡ�BPD=��DPC+��BPC����BPD=��A+��APD��
���DPC+��BPC=��A+��APD��
�ߡ�DPC=��A=�ȣ�
���BPC=��APD��
�֡ߡ�A=��B=�ȣ�
���ADP�ס�BPC��
��![]() ��
��
��ADBC=APBP��
(3)�⣺����ͼ������D��DE��AB�ڵ�E��
��AD=BD=10��AB=12��
��AE=BE=6
���ݹ��ɶ����ɵã�DE=![]() =8��
=8��
����DΪԲ�ģ���DCΪ�뾶��Բ��AB���У�
��DC=DE=8��
��BC=10-8=2��
��AD=BD��
���A=��B��
�֡ߡ�DPC=��A��
���DPC=��A=��B����(1)(2)�ľ����ADBC=APBP��
�֡�AP=t��BP=12-t��
��t(12-t)=10��2��
��t=2��t=10��
��t��ֵΪ2���10�룮