��Ŀ����
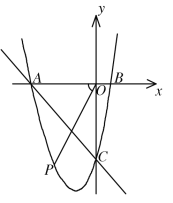
����Ŀ����2017����ʡʮ���У���24�⣬10�֣���֪OΪֱ��MN��һ�㣬OP��MN���ڵ���Rt��ABO�У���BAO=90�㣬AC��OP��OM��C��DΪOB���е㣬DE��DC��MN��E��
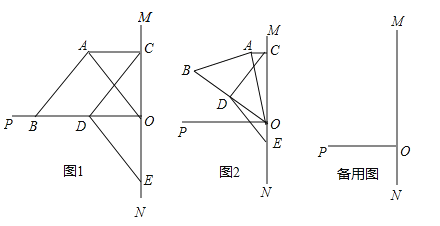
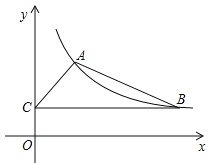
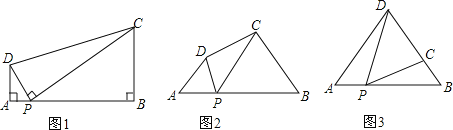
��1����ͼ1������B��OP�ϣ���
��AC OE�����������=����������
���߶�CA��CO��CD����ĵ�����ϵʽ�� ��
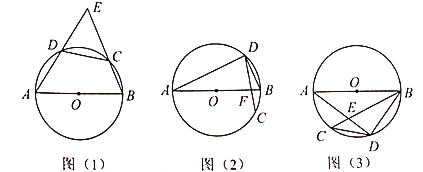
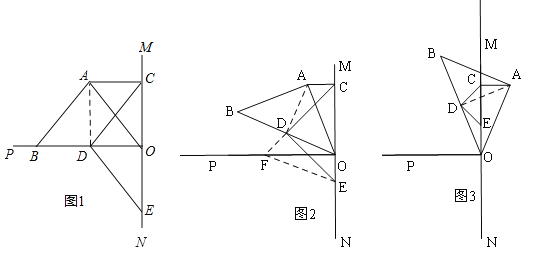
��2����ͼ1�еĵ���Rt��ABO��O��˳ʱ����ת����0�㣼����45�㣩����ͼ2����ô��1���еĽ��ۢ��Ƿ��������˵�����ɣ�
��3����ͼ1�еĵ���Rt��ABO��O��˳ʱ����ת����45�㣼����90�㣩��������ͼ3�л���ͼ�Σ���ֱ��д���߶�CA��CO��CD����ĵ�����ϵʽ ��
���𰸡���1����=����AC2+CO2=CD2����2������������3��OC��CA=![]() CD��
CD��
��������
���⣨1������ͼ1��֤��AC=OC��OC=OE�ɵý��ۣ�
�����ݹ��ɶ����ɵã�AC2+CO2=CD2��
��2����ͼ2����1���еĽ��������������������ߣ�����ȫ�������Σ�֤��A��D��O��C�ĵ㹲Բ������ACD=��AOB��ͬ���ã���EFO=��EDO����֤����ACO�ա�EOF����OE=AC��AO=EF�����ݹ��ɶ����ã�AC2+OC2=FO2+OE2=EF2����ֱ�������������Ϊб�߿ɵý��ۣ�
��3����ͼ3������AD����AD=OD֤����ACD�ա�OED��������CDE�ǵ���ֱ�������Σ���CE2=2CD2�����������ɵý��ۣ�OC��OE��2=��OC��AC��2=2CD2���������ǣ�OC��AC=![]() CD��
CD��
����������⣺��1����AC=OE������������
��ͼ1�����ڵ���Rt��ABO�У���BAO=90�㣬���ABO=��AOB=45�㣮��OP��MN�����COP=90�㣬���AOC=45�㣮��AC��OP�����CAO=��AOB=45�㣬��ACO=��POE=90�㣬��AC=OC������AD����BD=OD����AD=OD��AD��OB����AD��OC�����ı���ADOC�������Σ����DCO=45�㣬��AC=OD�����DEO=45�㣬��CD=DE����OC=OE����AC=OE��
����Rt��CDO����CD2=OC2+OD2����CD2=AC2+OC2��
�ʴ�ΪAC2+CO2=CD2��
��2����ͼ2����1���еĽ������������������ǣ�
����AD���ӳ�CD��OP��F������EF����AB=AO��DΪOB���е㣬��AD��OB�����ADO=90�㣮�ߡ�CDE=90�㣬���ADO=��CDE�����ADO����CDO=��CDE����CDO������ADC=��EDO���ߡ�ADO=��ACO=90�㣬���ADO+��ACO=180�㣬��A��D��O��C�ĵ㹲Բ�����ACD=��AOB��ͬ���ã���EFO=��EDO�����EFO=��AOC���ߡ�ABO�ǵ���ֱ�������Σ����AOB=45�㣬���DCO=45�㣬���COF����CDE�ǵ���ֱ�������Σ���OC=OF���ߡ�ACO=��EOF=90�㣬���ACO�ա�EOF����OE=AC��AO=EF����AC2+OC2=FO2+OE2=EF2��Rt��DEF�У�EF��DE=DC����AC2+OC2��DC2�����ԣ�1���еĽ�������������
��3����ͼ3�����ۣ�OC��CA=![]() CD�������ǣ�
CD�������ǣ�
����AD����AD=OD��ͬ������ADC=��EDO���ߡ�CAB+��CAO=��CAO+��AOC=90�㣬���CAB=��AOC���ߡ�DAB=��AOD=45�㣬���DAB����CAB=��AOD����AOC������DAC=��DOE�����ACD�ա�OED����AC=OE��CD=DE�����CDE�ǵ���ֱ�������Σ���CE2=2CD2���ࣨOC��OE��2=��OC��AC��2=2CD2����OC��AC=![]() CD���ʴ�ΪOC��AC=
CD���ʴ�ΪOC��AC=![]() CD��
CD��

 ��������һ���þ�ϵ�д�
��������һ���þ�ϵ�д� Сѧ��10����Ӧ����ϵ�д�
Сѧ��10����Ӧ����ϵ�д�