题目内容
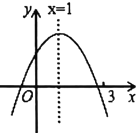
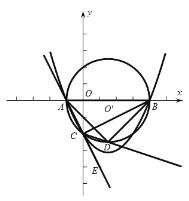
【题目】已知:二次函数![]() 的图象与
的图象与![]() 轴交于
轴交于![]() 两点,其中点
两点,其中点![]() ,与
,与![]() 轴负半轴交于点
轴负半轴交于点![]() ,起对称轴是直线
,起对称轴是直线![]() .
.
(1)求二次函数![]() 的解析式;
的解析式;
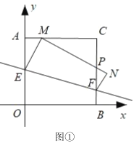
(2)圆![]() 经过点
经过点![]() 的外接圆,点
的外接圆,点![]() 是
是![]() 延长线上一点,
延长线上一点,![]() 的平分线交圆
的平分线交圆![]() 于点
于点![]() ,连接
,连接![]() 、
、![]() ,求
,求![]() 的面积;
的面积;
(3)在(2)的条件下,二次函数![]() 的图象上是否存在点
的图象上是否存在点![]() ,使得
,使得![]() ?如果存在,请求出所有符合条件的
?如果存在,请求出所有符合条件的![]() 点坐标;如果不存在,请说明理由.
点坐标;如果不存在,请说明理由.
【答案】(1)![]() ;(2)
;(2)![]() ;(3)存在,
;(3)存在,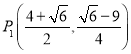 ,
,
【解析】
(1)根据抛物线的对称性,可以求出点B的坐标,再用待定系数法求解即可;
(2)根据![]() 以及圆的相关性质,可知△ABD为等腰直角三角形,从而得出
以及圆的相关性质,可知△ABD为等腰直角三角形,从而得出![]() 与
与![]() 的数量关系,列式求解即可;
的数量关系,列式求解即可;
(3)使得![]() 的点存在两种情况,利用相似导出线段之间的比值,再用直线和抛物线的解析式联立求得相关点的坐标.
的点存在两种情况,利用相似导出线段之间的比值,再用直线和抛物线的解析式联立求得相关点的坐标.
(1)∵点![]() ,对称轴为
,对称轴为![]()
∴![]()
将![]() 、
、![]() 、
、![]() 代入
代入![]() 中
中
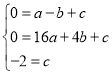
解得![]()
∴抛物线的解析式为:![]()
(2)∵![]() ,
,![]() ,
,![]()
∴![]() ,
,![]() ,
,![]() ,
,
∴![]()
又∵![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]()
∴![]() 为圆
为圆![]() 的直径,
的直径,![]() 点坐标为
点坐标为![]() ,
,
∴![]()
又∵![]() 平分
平分![]() ,
,
∴![]() ,
,
∴![]() ,
,![]() 为等腰直角三角形.
为等腰直角三角形.
连接![]() ,则
,则![]() ,
,![]() ,
,
∴![]() ,
,![]() 点坐标为
点坐标为![]()
设![]() 与
与![]() 轴交于点
轴交于点![]() ,
,
∵![]() ,
,
∴![]() ,
,
∴![]()
作![]() 轴于点
轴于点![]() ,
,
∵![]() ,
,
∴![]() ,
,![]()
∴![]() ;
;
(3)抛物线上存在点![]() ,使得
,使得![]() .分两种情况讨论:
.分两种情况讨论:

①过点![]() 作直线
作直线![]() ,交
,交![]() 轴于
轴于![]() .
.
∵![]() ,
,
∴![]() ,
,![]()
又∵![]() ,
,
∴![]() ,直线
,直线![]() 与抛物线在
与抛物线在![]() 点右侧的交点即为点
点右侧的交点即为点![]() .
.
∵![]() ,
,![]() ,
,
∴![]() ,
,
∴![]()
∵![]()
∴![]() ,
,![]() .
.
设直线![]() 的解析式为
的解析式为![]()
则有,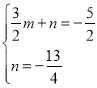
解得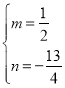 ,
,
直线![]() 的解析式为
的解析式为![]()
∴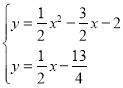
解得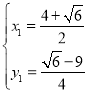 ,
,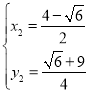 (舍)
(舍)
∴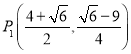
②过点![]() 作
作![]() ,交
,交![]() 轴于
轴于![]() 点.
点.
∵![]() ,
,
∴![]()
即直线![]() 与抛物线在
与抛物线在![]() 点右侧的交点即为
点右侧的交点即为![]() 点
点
又∵![]() ,
,
∴![]()
∴![]()
∴![]()
∴![]()
设直线![]() 的解析式为
的解析式为![]()
则有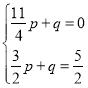 ,解得
,解得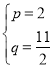 ,
,
∴直线![]() 的解析式为
的解析式为![]()
∴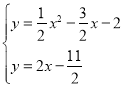 ,解得
,解得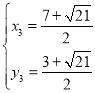 ,
,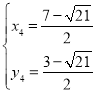 (舍)
(舍)
∴
∴符合条件的![]() 点有两个:
点有两个: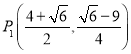 ,
, .
.

练习册系列答案
 培优好卷单元加期末卷系列答案
培优好卷单元加期末卷系列答案
相关题目