题目内容
【题目】已知△ABC,以AC为边在△ABC外作等腰△ACD,其中AC=AD
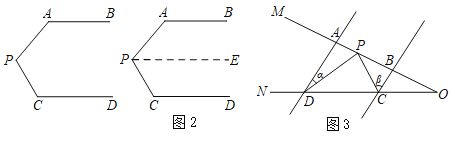
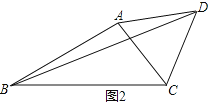
(1) 如图1,若AB为边在△ABC外作△ABE,AB=AE,∠DAC=∠EAB=60°,求∠BFC的度数
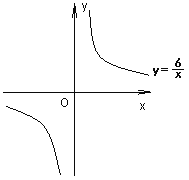
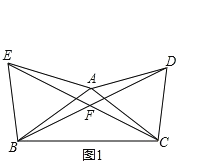
(2) 如图2,∠ABC=α,∠ACD=β,BC=6,BD=8
① 若α=30°,β=60°,AB的长为
② 若改变α、β的大小,但α+β=90°,求△ABC的面积
【答案】 (1) 120°;(2) ①![]() ;②
;② ![]() .
.
【解析】分析:(1)根据SAS,可首先证明△AEC≌△ABD,再利用全等三角形的性质,可得对应角相等,根据三角形的外角的定理,可求出∠BFC的度数;
(2)①如图2,在△ABC外作等边△BAE,连接CE,利用旋转法证明△EAC≌△BAD,可证∠EBC=90°,EC=BD=8,因为BC=6,在Rt△BCE中,由勾股定理求BE即可;
②过点B作BE∥AH,并在BE上取BE=2AH,连接EA,EC.并取BE的中点K,连接AK,仿照(2)利用旋转法证明△EAC≌△BAD,求得EC=DB,利用勾股定理即可求解.
本题解析:
(1)如图1,
∵AE=AB,AD=AC,
∵∠EAB=∠DAC=60,
∴∠EAC=∠EAB+∠BAC,∠DAB=∠DAC+∠BAC,
∴∠EAC=∠DAB,
在△AEC和△ABD中,
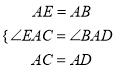 ,
,
∴△AEC≌△ABD(SAS),
∴∠AEC=∠ABD,
∵∠BFC=∠BEF+∠EBF=∠AEB+∠ABE,
∴∠BFC=∠AEB+∠ABE=120;
(2)①如图2,以AB为边在△ABC外作正三角形ABE,连接CE.
由(1)可知△EAC≌△BAD.
∴EC=BD.
∴EC=BD=8,
∵∠BAE=60,∠ABC=30,
∴∠EBC=90.
在Rt△EBC中,EC=8,BC=6,
∴EB=![]() ,
,
∴AB=BE=![]() .
.
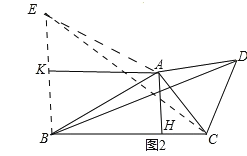
②如图2,作AH⊥BC交BC于H,过点B作BE∥AH,并在BE上取BE=2AH,连接EA,EC.并取BE的中点K,连接AK.
∵AH⊥BC于H,
∴∠AHC=90°.
∵BE∥AH,
∴∠EBC=90°.
∵∠EBC=90°,BE=2AH,
∴EC2=EB +BC =4AH +BC.
∵K为BE的中点,BE=2AH,
∴BK=AH.
∵BK∥AH,
∴四边形AKBH为平行四边形。
又∵∠EBC=90°,
∴四边形AKBH为矩形.∠ABE=∠ACD,
∴∠AKB=90.
∴AK是BE的垂直平分线。
∴AB=AE.
∵AB=AE,AC=AD,∠ABE=∠ACD
∴∠EAB=∠DAC,
∴∠EAB+∠EAD=∠DAC+∠EAD,
即∠EAC=∠BAD,
在△EAC与△BAD中,
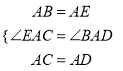 ,
,
∴△EAC≌△BAD.
∴EC=BD=8.
在Rt△BCE中,BE=![]() ,
,
∴AH=![]() BE=
BE=![]() ,
,
∴S△ABC=![]() BCAH=3
BCAH=3![]() .
.
故答案为:2![]() .
.

 春雨教育同步作文系列答案
春雨教育同步作文系列答案