题目内容
【题目】在平面直角坐标系中,![]() 为原点,抛物线
为原点,抛物线![]() 经过点
经过点![]() ,对称轴为直线
,对称轴为直线![]() ,点
,点![]() 关于直线
关于直线![]() 的对称点为点
的对称点为点![]() .过点
.过点![]() 作直线
作直线![]() 轴,交
轴,交![]() 轴于点
轴于点![]() .
.
(Ⅰ)求该抛物线的解析式及对称轴;
(Ⅱ)点![]() 在
在![]() 轴上,当
轴上,当![]() 的值最小时,求点
的值最小时,求点![]() 的坐标;
的坐标;
(Ⅲ)抛物线上是否存在点![]() ,使得
,使得![]() ,若存在,求出点
,若存在,求出点![]() 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.
【答案】(Ⅰ)抛物线的解析式为![]() ;抛物线的对称轴为直线
;抛物线的对称轴为直线![]() ;(Ⅱ)
;(Ⅱ)![]() 点坐标为
点坐标为![]() ;(Ⅲ)存在,
;(Ⅲ)存在,![]() 点坐标为
点坐标为![]() 或
或![]() ,理由见解析
,理由见解析
【解析】
(Ⅰ)将![]() 点代入二次函数的解析式,即可求出a,再根据对称轴的公式即可求解.
点代入二次函数的解析式,即可求出a,再根据对称轴的公式即可求解.
(Ⅱ)先求出B点胡坐标,要求![]() 胡最小值,只需找到B关于轴的对称点
胡最小值,只需找到B关于轴的对称点![]() ,则直线A
,则直线A![]() 与y轴的交点就是点P,根据待定系数法求出AB1的解析式,令y=0,即可求出P点的坐标.
与y轴的交点就是点P,根据待定系数法求出AB1的解析式,令y=0,即可求出P点的坐标.
(Ⅲ)设点Q的坐标,并求出△AOQ面积,从而得到△AOQ面积,根据Q点胡不同位置进行分类,用m及割补法求出面积方程,即可求解.
(Ⅰ)∵![]() 经过点
经过点![]() ,
,
∴![]() ,解得
,解得![]() ,
,
∴抛物线的解析式为![]() ,
,
∵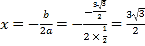 ,
,
∴抛物线的对称轴为直线![]() .
.
(Ⅱ)∵点![]() ,对称轴为
,对称轴为![]() ,
,
∴点![]() 关于对称轴的对称点
关于对称轴的对称点![]() 点坐标为
点坐标为![]() .
.
作点![]() 关于轴的对称点
关于轴的对称点![]() ,得
,得![]() ,
,
设直线AB1的解析式为![]() ,
,
把点![]() ,点
,点![]() 代入得
代入得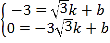 ,
,
解得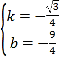 ,∴
,∴![]() .
.
∴直线![]() 与
与![]() 轴的交点即为
轴的交点即为![]() 点.
点.
令![]() 得
得![]() ,
,
∵![]() 点坐标为
点坐标为![]() .
.
(Ⅲ)∵![]() ,
,![]() 轴,∴
轴,∴![]() ,
,![]() ,
,
∴![]() ,
,
又∵![]() ,∴
,∴![]() .
.
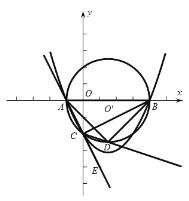
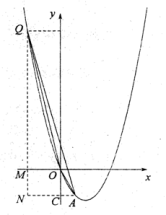
设![]() 点坐标为
点坐标为![]() ,
,
如图情况一,作![]() ,交
,交![]() 延长线于点
延长线于点![]() ,
,
∵![]() ,
,
∴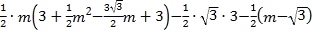
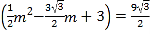 ,
,
化简整理得![]() ,
,
解得![]() ,
,![]() .
.

如图情况二,作![]() ,交
,交![]() 延长线于点
延长线于点![]() ,交
,交![]() 轴于点
轴于点![]() ,
,
∵![]() ,
,
∴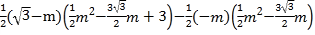
![]() ,
,
化简整理得![]() ,
,
解得![]() ,
,![]() ,
,
∴![]() 点坐标为
点坐标为![]() 或
或![]() ,
,
∴抛物线上存在点![]() ,使得
,使得![]() .
.

练习册系列答案
 字词句篇与同步作文达标系列答案
字词句篇与同步作文达标系列答案
相关题目