题目内容
【题目】求函数![]() 的最值.
的最值.
【答案】①|b|>1,y极大值=![]() ,y极小值=
,y极小值=![]() ;②|b|<1, y极大值=
;②|b|<1, y极大值=![]() ;y极小值=
;y极小值=![]() ,③当ab>1时,y极大值=
,③当ab>1时,y极大值=![]() ;ab<1时,y极小值=
;ab<1时,y极小值=![]() .
.
【解析】
将函数y=![]() 化为关于x的一元二次方程:(1-y)x2+2(a-by)x+(1-y)=0,从而得出△≥0,将本题视为在△≥0的情况下求y的最值,然后讨论b的范围,在b不同范围内求出y的最值.
化为关于x的一元二次方程:(1-y)x2+2(a-by)x+(1-y)=0,从而得出△≥0,将本题视为在△≥0的情况下求y的最值,然后讨论b的范围,在b不同范围内求出y的最值.
把 y=![]() 化为关于x的二次方程(1﹣y)x2+2(a﹣by)x+(1﹣y)=0,
化为关于x的二次方程(1﹣y)x2+2(a﹣by)x+(1﹣y)=0,
∵△=(b2﹣1)y2﹣2(ab﹣1)y+a2﹣1≥0,
①b2﹣1>0,即|b|>1,
∴y=![]() ,可得y≤
,可得y≤![]() 或y≥
或y≥![]() ,
,
∴y极大值=![]() ,
,
y极小值=![]() ;
;
②b2﹣1<0,即|b|<1,则有![]() ≤y≤
≤y≤![]() ,
,
∴y极大值=![]() ;
;
y极小值=![]() ,
,
③b2﹣1=0,即|b|=1,得(ab-1)y≤![]() ,
,
当ab>1时,y≤![]() ,∴y极大值=
,∴y极大值=![]() ;
;
ab<1时,y≥![]() ,∴y极小值=
,∴y极小值=![]() .
.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
【题目】如图,AB是⊙O的直径,C是AB延长线上一点,CD与⊙O相切于点E,AD⊥CD于点D.
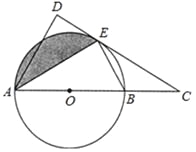
(1)求证:AE平分∠DAC;
(2)若AB=4,∠ABE=60°.
①求AD的长;
②求出图中阴影部分的面积.
【题目】九(1)班数学兴趣小组经过市场调查,整理出某种商品在第x(1≤x≤90)天的售价与销售量的相关信息如下表:
时间x(天) | 1≤x<50 | 50≤x≤90 |
售价(元/件) | x+40 | 90 |
每天销量(件) | 200-2x | |
已知该商品的进价为每件30元,设销售该商品的每天利润为y元[
(1)求出y与x的函数关系式;
(2)问销售该商品第几天时,当天销售利润最大,最大利润是多少?
(3)该商品在销售过程中,共有多少天每天销售利润不低于4800元?请直接写出结果.