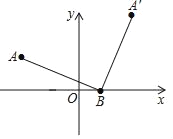
题目内容
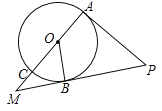
【题目】如图，AB是⊙O的直径，C是AB延长线上一点，CD与⊙O相切于点E，AD⊥CD于点D．
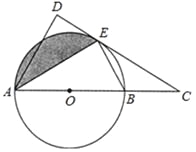
（1）求证：AE平分∠DAC；
（2）若AB=4，∠ABE=60°．
①求AD的长；
②求出图中阴影部分的面积.
【答案】
【解析】试题分析：（1）证明：连接OE。
∵CD是⊙O的切线，∴OE⊥CD。
∵AD⊥CD，∴AD∥OE。∴∠DAE=∠AEO。
∵OA=OE，∴∠EAO=∠AEO。
∴∠DAE=∠EAO。∴AE平分∠DAC。
（2）①∵AB是⊙O的直径，∴∠AEB=90°。
∵∠ABE=60°，∴∠EAO=30°。∴∠DAE=∠EAO=30°。
∵AB=6，∴在Rt△ABE中，BE=
="3," AE=
在Rt△ADE中，∵∠DAE=30°，AE=，∴
。
②连接OE ∵∠EAO=∠AEO=30°，∴
。
∵OA=OB，∴
。
∴
。
练习册系列答案
相关题目
【题目】某县盛产苹果，春节期问，一外地经销商安排
辆汽年装运
、
、
三种不同品质的苹果
吨到外地销售，按计划辆汽年都要装满且每辆汽车只能装同一种品质的苹果，每辆汽车的运载量及每吨苹果的获利如下表：
苹果品种 |
|
|
|
每辆汽车运载数 |
|
|
|
每吨获利（元） |
|
|
|
（1）设装运种苹果的车辆数为
辆，装运种苹果车辆数为
辆，据上表提供的信息，求出
与之间的函数关系式；
（2）为了减少苹果的积压，县林业局制定出台了促进销售的优惠政策，在外地经销商原有获利不变情况下，政府对外地经销商按每吨
元的标准实行运费补贴若种苹果的车辆数满足
.若要使该外地经销商所获利
（元）最大，应采用哪种车辆安排方案?并求出最大利润（元）的最大值．
