题目内容
【题目】如图，为测量某建筑物EF的高度，小明在楼AB上选择观测点A、C，从A测得建筑物的顶部E的仰角为37°，从C测得建筑物的顶部E的仰角为45°，A处高度为20m，C处高度为10m．求建筑物EF的高度（精确到1m）．
（参考数据：sin37°≈0.6，cos37°≈0.8，tan37≈0.75，
≈1.4）
【答案】50m．
【解析】
设CH＝xm，根据矩形的性质得到AG＝CH＝x，根据正切的定义用x表示出EH、EG，结合图形列式计算即可．
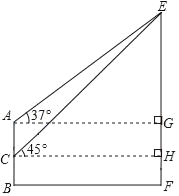
解：设CH＝xm，由题意得，四边形ACHG为矩形，
∴AG＝CH＝x，GH＝AC＝20﹣10＝10，
∵∠ECH＝45°，
∴EH＝CH＝x，
在Rt△EAG中，tan∠EAG＝
，即tan37°＝
，
解得，EG≈
x，
则x﹣x＝10，
解得，x＝40，
∴EF＝FH+EH＝50，
答：建筑物EF的高度约为50m．
练习册系列答案
相关题目
