题目内容
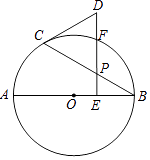
【题目】如图1,点O为直线AB上一点,过点O作射线OC,使∠AOC:∠BOC=2:1,将直角三角板的直角顶点放在点O处,一边ON在射线OA上,另一边OM在直线AB的下方.
(1)在图1中,∠AOC= °,∠MOC= °;
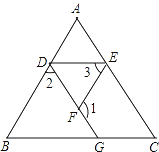
(2)将图1中的三角板按图2的位置放置,使得OM在射线QA上,求∠CON的度数;
(3)将上述直角三角板按图3的位置放置,OM在∠BOC的内部,说明∠BON﹣∠COM的值固定不变.

【答案】(1)120,150;(2)30°;(3)30°.
【解析】
(1)点O为直线AB上一点,过点O作射线OC,使∠AOC:∠BOC=2:1,可以求得∠AOC和∠MOC的度数;
(2)根据∠AOC的度数和∠MON的度数可以得到∠CON的度数;
(3)根据∠BOC=60°,∠MON=90°,∠BON=∠MON﹣∠BOM,∠COM=∠BOC﹣∠BOM,可以得到∠BON﹣∠COM的度数.
解:(1)∵点O为直线AB上一点,过点O作射线OC,使∠AOC:∠BOC=2:1,∠AOC+∠BOC=180°,
∴∠AOC=120°,∠BOC=60°,
∵∠BOM=90°,
∴∠MOC=150°,
故答案为:120,150;
(2)∵由(1)可知:∠AOC=120°,∠MON=90°,∠AOC=∠MON+∠CON,
∴∠CON=∠AOC﹣∠MON=120°﹣90°=30°;
(3)由图可知:∠BOC=60°,∠MON=90°,∠BON=∠MON﹣∠BOM,∠COM=∠BOC﹣∠BOM,
则,∠BON﹣∠COM=90°﹣∠BOM﹣(60°﹣∠BOM)=30°,
即∠BON﹣∠COM的度数是30°.

 培优好卷单元加期末卷系列答案
培优好卷单元加期末卷系列答案【题目】下面是某同学对多项式(x2-4x+2)(x2-4x+6)+4进行因式分解的过程.
解:设x2-4x=y
原式=(y+2)(y+6)+4 (第一步)
=y2+8y+16 (第二步)
=(y+4)2(第三步)
=(x2-4x+4)2(第四步)
回答下列问题:
(1)该同学第二步到第三步运用了因式分解的_______.
A.提取公因式 |
B.平方差公式 |
C.两数和的完全平方公式 |
D.两数差的完全平方公式 |
(2)该同学因式分解的结果是否彻底?________.(填“彻底”或“不彻底”)若不彻底,请直接写出因式分解的最后结果_________ .
(3)请你模仿以上方法尝试对多项式(x2-2x)(x2-2x+2)+1进行因式分解.