题目内容
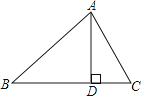
【题目】如图，梯形ABCD中，AB∥DC ， ∠B=90°，E为BC上一点，且AE⊥ED ． 若BC=12，DC=7，BE：EC=1：2，
（1）求AB的长．
（2）求△AED的面积
【答案】
（1）
解答：∵AB∥DC，且∠B=90°，
∴∠AEB+∠BAE=90°及∠C=90度．
∴∠AEB+∠CED=90度．
故∠BAE=∠CED．
∴△EAB∽△DEC．
∴ 
= 
又BE：EC=1：2，且BC=12及DC=7，
故 
= 
则AB= 
（2）
解答：∵△EAB∽△DEC，
∴ ＝
即： 
= 
解得：CD=7
∴S△AED=S梯形ABCD-S△ABE-S△ECD= 
（AB+CD）BC- ABBE- ECCD=
（ +7）12- × ×4- ×8×7= 
【解析】（1）由题意易知AB和CD所在的两个三角形相似，再利用相似比即可求出所求线段的长度．（2）根据证得的△EAB∽△DEC利用相似三角形对应边的比成比例求得线段CD的长，利用梯形的面积减去两个三角形的面积即可求得三角形AED的面积．
【考点精析】掌握相似三角形的判定与性质是解答本题的根本，需要知道相似三角形的一切对应线段(对应高、对应中线、对应角平分线、外接圆半径、内切圆半径等）的比等于相似比；相似三角形周长的比等于相似比；相似三角形面积的比等于相似比的平方．
练习册系列答案
相关题目
