题目内容
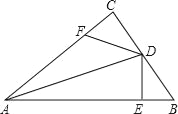
【题目】如图,△ABC是等边三角形,点D、E分别在BC、AC上,且BD=CE , AD与BE相交于点F . 
(1)试说明△ABD≌△BCE;
(2)△EAF与△EBA相似吗?说说你的理由.
【答案】
(1)证明:∵△ABC是等边三角形,
∴AB=BC,∠ABD=∠BCE=∠BAC,
又∵BD=CE,
∴△ABD≌△BCE;
(2)解:相似;
理由如下:
∵△ABD≌△BCE,
∴∠BAD=∠CBE,
∴∠BAC-∠BAD=∠CBA-∠CBE,
∴∠EAF=∠EBA,又∵∠AEF=∠BEA,
∴△EAF∽△EBA.
【解析】(1)根据等边三角形各边长相等和各内角为60°的性质可以求证△ABD≌△BCE;(2)根据全等三角形对应角相等性质可得∠BAD=∠CBE , 进而可以求得∠EAF=∠EBA , 即可求证△EAF∽△EBA , 即可解题.
【考点精析】认真审题,首先需要了解相似三角形的判定(相似三角形的判定方法:两角对应相等,两三角形相似(ASA);直角三角形被斜边上的高分成的两个直角三角形和原三角形相似; 两边对应成比例且夹角相等,两三角形相似(SAS);三边对应成比例,两三角形相似(SSS)).

练习册系列答案
相关题目