题目内容
【题目】如图,反比例函数![]() (x>0)的图象经过点A(2
(x>0)的图象经过点A(2![]() ,1),直线AB与反比例函数图象交与另一点B(1,a),射线AC与y轴交于点C,∠BAC=75°,AD⊥y轴,垂足为D.
,1),直线AB与反比例函数图象交与另一点B(1,a),射线AC与y轴交于点C,∠BAC=75°,AD⊥y轴,垂足为D.
(1)求反比例函数的解析式;
(2)求tan∠DAC的值及直线AC的解析式.

【答案】(1)反比例函数为y=![]() (x>0);(2)tan∠DAC=
(x>0);(2)tan∠DAC=![]() ;直线AC的解析式为y=
;直线AC的解析式为y=![]() x﹣1.
x﹣1.
【解析】
试题(1)根据反比例函数图象上点的坐标特征易得k=2![]() , 从而求得反比例函数解析式;
, 从而求得反比例函数解析式;
(2)作BH⊥AD于H,如图,根据反比例函数图象上点的坐标特征确定B点坐标为(1,2![]() ),确定AH=2
),确定AH=2![]() ﹣1,BH=2
﹣1,BH=2![]() ﹣1,可判断△ABH为等腰直角三角形,所以∠BAH=45°,得到∠DAC=∠BAC﹣∠BAH=30°,根据特殊角的三角函数值得tan∠DAC=
﹣1,可判断△ABH为等腰直角三角形,所以∠BAH=45°,得到∠DAC=∠BAC﹣∠BAH=30°,根据特殊角的三角函数值得tan∠DAC=![]() ;由于AD⊥y轴,则OD=1,AD=2
;由于AD⊥y轴,则OD=1,AD=2![]() , 然后在Rt△OAD中利用正切的定义可计算出CD=2,易得C点坐标为(0,﹣1),于是可根据待定系数法求出直线AC的解析式为y=
, 然后在Rt△OAD中利用正切的定义可计算出CD=2,易得C点坐标为(0,﹣1),于是可根据待定系数法求出直线AC的解析式为y=![]() x﹣1.
x﹣1.
试题解析:(1)由反比例函数y=![]() (x>0)的图象经过点A(2
(x>0)的图象经过点A(2![]() ,1),得:k=2
,1),得:k=2![]() ×1=2
×1=2![]() ,
,
∴反比例函数为y=![]() (x>0);
(x>0);
(2)作BH⊥AD于H,如图,
把B(1,a)代入反比例函数解析式y=![]() (x>0),得a=2
(x>0),得a=2![]() ,
,
∴B点坐标为(1,2![]() ),
),
∴AH=2![]() ﹣1,BH=2
﹣1,BH=2![]() ﹣1,
﹣1,
∴△ABH为等腰直角三角形,
∴∠BAH=45°,
∵∠BAC=75°,
∴∠DAC=∠BAC﹣∠BAH=30°,
∴tan∠DAC=tan30°=![]() ;
;
∵AD⊥y轴,
∴OD=1,AD=2![]() ,
,
∵tan∠DAC=![]() =
=![]() ,
,
∴CD=2,
∴OC=1,
∴C点坐标为(0,﹣1),
设直线AC的解析式为y=kx+b,
把A(2![]() ,1)、C(0,﹣1)代入
,1)、C(0,﹣1)代入
得![]() ,解得:
,解得: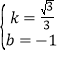 ,
,
∴直线AC的解析式为y=![]() x﹣1;
x﹣1;