题目内容
【题目】如图,在![]() 和
和![]() 中,
中,![]() 、
、![]() 、
、![]() 、
、![]() 在同一直线上,下面有四个条件:
在同一直线上,下面有四个条件:
①![]() ;②
;②![]() ;③
;③![]() ;④
;④![]() .请你从中选三个作为题设,余下的一个作为结论,写出一个真命题,并加以证明.
.请你从中选三个作为题设,余下的一个作为结论,写出一个真命题,并加以证明.
解:我写的真命题是:
已知:____________________________________________;
求证:___________.(注:不能只填序号)
证明如下:
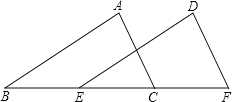
【答案】已知:如图,在△ABC和△DEF中,B、E、C、F在同一直线上,AB=DE,AC=DF,BE=CF.求证:AB∥DE.证明见解析.或已知:如图,在△ABC和△DEF中,B、E、C、F在同一直线上,AB=DE,AB∥DE,BE=CF.求证:AC=DF.证明见解析.
【解析】
由BE=CFBC=EF,所以,由①②④,可用SSS△ABC≌△DEF∠ABC=∠DEF AB∥DE;由①③④,可用SAS△ABC≌△DEFAC=DF;由于不存在ASS的证明全等三角形的方法,故由其它三个条件不能得到1或4.
解:将①②④作为题设,③作为结论,可写出一个正确的命题,如下:
已知:如图,在△ABC和△DEF中,B、E、C、F在同一直线上,AB=DE,AC=DF,BE=CF.
求证:AB∥DE.
证明:在△ABC和△DEF中,
∵BE=CF,
∴BC=EF.
又∵AB=DE,AC=DF,
∴△ABC≌△DEF(SSS)
∴∠ABC=∠DEF.
∴ AB∥DE.
将①③④作为题设,②作为结论,可写出一个正确的命题,如下:
已知:如图,在△ABC和△DEF中,B、E、C、F在同一直线上,AB=DE,AB∥DE,BE=CF.
求证:AC=DF.
证明:∵AB∥DE,∴∠ABC=∠DEF.
在△ABC和△DEF中
∵BE=CF,∴BC=EF.
又∵AB=DE,∠ABC=∠DEF,
∴△ABC≌△DEF(SAS),
∴AC=DF.

【题目】某超市计划购进甲、乙两种商品,两种商品的进价、售价如下表:
商品 | 甲 | 乙 |
进价(元/件) |
|
|
售价(元/件) | 200 | 100 |
若用360元购进甲种商品的件数与用180元购进乙种商品的件数相同.
(1)求甲、乙两种商品的进价是多少元?
(2)若超市销售甲、乙两种商品共50件,其中销售甲种商品为![]() 件(
件(![]() ),设销售完50件甲、乙两种商品的总利润为
),设销售完50件甲、乙两种商品的总利润为![]() 元,求
元,求![]() 与
与![]() 之间的函数关系式,并求出
之间的函数关系式,并求出![]() 的最小值.
的最小值.