��Ŀ����
����Ŀ�����ⱳ�����ڡ�ABC�У�AB��BC��AC���ߵij��ֱ�Ϊ![]() ������������ε������С��ͬѧ�ڽ�������ʱ���Ƚ���һ������������ÿ��С�����εı߳�Ϊ1�������������л�����㣨���������㶼��С�����εĶ��㴦������ͼ��ʾ����������Ҫ��ߣ�������������ܼ��������������뽫��ABC�����ֱ����д�ں������� ����
������������ε������С��ͬѧ�ڽ�������ʱ���Ƚ���һ������������ÿ��С�����εı߳�Ϊ1�������������л�����㣨���������㶼��С�����εĶ��㴦������ͼ��ʾ����������Ҫ��ߣ�������������ܼ��������������뽫��ABC�����ֱ����д�ں������� ����
˼ά��չ�����ǰ��������ABC����ķ���������ͼ��������ABC�У�AB��BC��AC���߳��ֱ�Ϊ![]() ��2
��2![]() ��a��0����������ͼ��������������ÿ��С�����εı߳�Ϊa��������Ӧ�ġ�ABC��ֱ��д��������������ϵĸ����� ����
��a��0����������ͼ��������������ÿ��С�����εı߳�Ϊa��������Ӧ�ġ�ABC��ֱ��д��������������ϵĸ����� ����

���𰸡����ⱳ���� ![]() ��˼ά��չ��
��˼ά��չ�� ![]() a��
a��
��������
���ⱳ�������ݷָ�������ε������
˼ά��չ��![]() a��ֱ�DZ߳�Ϊa��2a��ֱ�������ε�б�ߣ�2
a��ֱ�DZ߳�Ϊa��2a��ֱ�������ε�б�ߣ�2![]() ��ֱ�DZ߳�Ϊ2a��2a��ֱ�������ε�б�ߣ�
��ֱ�DZ߳�Ϊ2a��2a��ֱ�������ε�б�ߣ�![]() ��ֱ�DZ߳�Ϊa��4a��ֱ�������ε�б�ߣ���������Ϊһ�����ε������ȥ����ֱ�������ε����������ͼ��BH��AC��H�������������⼴�ɣ�
��ֱ�DZ߳�Ϊa��4a��ֱ�������ε�б�ߣ���������Ϊһ�����ε������ȥ����ֱ�������ε����������ͼ��BH��AC��H�������������⼴�ɣ�
�⣺���ⱳ����S��ABC��3��3��![]() ��1��2��
��1��2��![]() ��1��3��
��1��3��![]() ��2��3��
��2��3��![]() ��
��
˼ά��չ����ͼ��BH��AC��H��
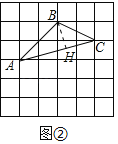
��S��ABC��![]() ACBH��2a��4a��
ACBH��2a��4a��![]() ��2a��2a��
��2a��2a��![]() ��a��2a��
��a��2a��![]() ��a��4a��3a2��
��a��4a��3a2��
��![]() ��
��![]() a��BH��3a2��
a��BH��3a2��
��BH��![]() a��
a��

����Ŀ��ij���мƻ������ס���������Ʒ��������Ʒ�Ľ��ۡ��ۼ����±���
��Ʒ | �� | �� |
���ۣ�Ԫ/���� |
|
|
�ۼۣ�Ԫ/���� | 200 | 100 |
����360Ԫ����������Ʒ�ļ�������180Ԫ����������Ʒ�ļ�����ͬ��
��1����ס���������Ʒ�Ľ����Ƕ���Ԫ��
��2�����������ۼס���������Ʒ��50�����������ۼ�����ƷΪ![]() ����
����![]() ������������50���ס���������Ʒ��������Ϊ
������������50���ס���������Ʒ��������Ϊ![]() Ԫ����
Ԫ����![]() ��
��![]() ֮��ĺ�����ϵʽ�������
֮��ĺ�����ϵʽ�������![]() ����Сֵ��
����Сֵ��




