题目内容
【题目】如图，
，
，
，则下列结论中：①
；②
；③
；④
；正确的是（ ）
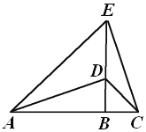
A.①②③B.①②④C.①③④D.②③④
【答案】B
【解析】
延长CD交AE于点F，由
，得：∠ABD=∠EBC=90°，BD=BC，AB=EB，即可判断①；延长AD交CE于点M，由，得∠BAD=∠BEC，进而得到∠AMC=90°，即可判断②；根据勾股定理，求出CD和AE的值，即可判断③；由∠EAD+∠BAD=45°，∠BEC+∠ECD=∠BDC=45°，即可判断④.
延长CD交AE于点F，
∵
∴∠ABD=∠EBC=90°，BD=BC，AB=EB，
∴∠EDF=∠BDC=∠BCD=45°，∠AEB=∠EAB=45°，
∴∠EFD=180°-45°-45°=90°，
∴
，
故①正确；
延长AD交CE于点M，
∵
∴∠BAD=∠BEC，
∵∠BEC+∠BCE=180°-∠EBC=180°-90°=90°，
∴∠BAD +∠BCE=90°，
∴∠AMC=90°，即：
，
故②正确；
∵在等腰RtBCD中，
，
∴
，
同理：
，
∴
，
故③错误；
∵在等腰RtABE中，∠EAD+∠BAD=45°，
又∵∠BEC+∠ECD=∠BDC=45°，∠BAD=∠BEC，
∴
，
故④正确.
故选B.
练习册系列答案
相关题目
【题目】某超市计划购进甲、乙两种商品，两种商品的进价、售价如下表：
商品 | 甲 | 乙 |
进价（元/件） |
|
|
售价（元/件） | 200 | 100 |
若用360元购进甲种商品的件数与用180元购进乙种商品的件数相同．
（1）求甲、乙两种商品的进价是多少元？
（2）若超市销售甲、乙两种商品共50件，其中销售甲种商品为
件（
），设销售完50件甲、乙两种商品的总利润为
元，求与之间的函数关系式，并求出的最小值．
