题目内容
【题目】如图，在平面直角坐标系中，A、B两点分别在x轴和y轴上，OA=1，OB= 
，连接AB，过AB中点C1分别作x轴和y轴的垂线，垂足分别是点A1、B1 ， 连接A1B1 ， 再过A1B1中点C2作x轴和y轴的垂线，照此规律依次作下去，则点Cn的坐标为 ． 
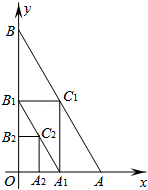
【答案】
【解析】解：∵过AB中点C1分别作x轴和y轴的垂线，垂足分别是点A1、B1 ，
∴B1C1和C1A1是三角形OAB的中位线，
∴B1C1= 
OA= ，C1A1= OB= 
，
∴C1的坐标为（ ， ），
同理可求出B2C2= 
= 
，C2A2= 
= 
∴C2的坐标为（ ， ），
…以此类推，
可求出BnCn= 
，CnAn= 
，
∴点Cn的坐标为 ，
故答案为： ．
首先利用三角形中位线定理可求出B1C1的长和C1A1的长，即C1的横坐标和纵坐标，以此类推即可求出点Cn的坐标．
练习册系列答案
相关题目
