��Ŀ����
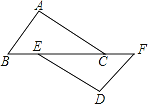
����Ŀ����ͼ���ڡ�ABC�� ����A=��B��D��E�DZ�AB�ϵĵ㣬DG��AC��EF��BC��DG��EF�� ���ڵ�H��
(1)��HDE���HED�Ƿ���ȣ���˵�����ɣ�
��:��HDE=��HED���������£�
��DG��AC(��֪)
���� �������� ���� �� ���� ���� ������
�� EF��BC (��֪)
������ ������ ���� �� �� ����
�֡ߡ�A=��B (��֪)
�� �� �� ��.
(2)�����C=90�㣬DG�� EF�к�λ�ù�ϵ�������� (1)�еĽ��˵�����ɣ�
�⣺�������������������������£�
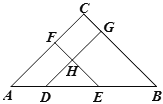
���𰸡���1������������2��DG��EF�����ɼ�����.
��������
(1)����ƽ���ߵ�������֤��A=��HDE����B=��HED���ɡ�A=��B���ɵó���HDE=��HED��
(2)��EF��BC�ó���AFE=��C����DG��AC�ó���DHE=��AFE���Ӷ��ó�DG��EF.
�⣺(1)��HDE=����ED���������£�
��DG��AC(��֪)
������A����HDE (����ֱ��ƽ�У�ͬλ����ȡ�)
�� EF�� BC(��֪)
������B����HED (����ֱ��ƽ�У�ͬλ����ȡ�)
�֡ߡ�A=��B(��֪)
�� ��HDE ����HED �� �������� ��.
��2����DG��EF�����������£�
��EF��BC��
���AFE����C��90�㣬
��AC��DG��
���DHE����AFE��90�㣬
��DG��EF.