题目内容
【题目】如图1,在△ABC中,∠ACB=90°,∠CAB=30°,△ABD是等边三角形,E是AB的中点,连接CE并延长交AD于F.
(1)求证:△AEF≌△BEC;
(2)判断四边形BCFD是何特殊四边形,并说出理由;
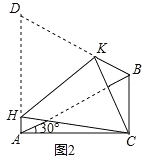
(3)如图2,将四边形ACBD折叠,使D与C重合,HK为折痕,若BC=1,求AH的长.

【答案】(1)(2)见解析;(3)![]()
【解析】试题分析:(1)在△ABC中,由已知可得∠ABC=60°,从而推得∠BAD=∠ABC=60°.由E为AB的中点,得到AE=BE.又因为∠AEF=∠BEC,所以△AEF≌△BEC;(2)在Rt△ABC中,E为AB的中点,则CE=![]() AB,BE=
AB,BE=![]() AB,得到∠BCE=∠EBC=60°.由△AEF≌△BEC,得∠AFE=∠BCE=60°.又∠D=60°,得∠AFE=∠D=60度.所以FC∥BD,又因为∠BAD=∠ABC=60°,所以AD∥BC,即FD∥BC,则四边形BCFD是平行四边形.
AB,得到∠BCE=∠EBC=60°.由△AEF≌△BEC,得∠AFE=∠BCE=60°.又∠D=60°,得∠AFE=∠D=60度.所以FC∥BD,又因为∠BAD=∠ABC=60°,所以AD∥BC,即FD∥BC,则四边形BCFD是平行四边形.
(2)由∠BAD=60°,∠CAB=30°,可得∠CAH=90°;在Rt△ABC中,∠CAB=30°,BC=1,根据30°角的直角三角形的性质可得AB=2BC=2,所以AD=AB=2.设AH=x,则HC=HD=AD﹣AH=2﹣x,在Rt△ABC中,由勾股定理求得AC2=3,在Rt△ACH中,根据勾股定理列出方程x2+3=(2﹣x)2,解方程即可求得AH的值.
试题解析:
(1)证明:①在△ABC中,∠ACB=90°,∠CAB=30°,∴∠ABC=60°.
在等边△ABD中,∠BAD=60°,∴∠BAD=∠ABC=60°.
∵E为AB的中点,∴AE=BE.又∵∠AEF=∠BEC,∴△AEF≌△BEC.
(2)在△ABC中,∠ACB=90°,E为AB的中点,
∴CE=![]() AB,BE=
AB,BE=![]() AB.∴CE=AE,∴∠EAC=∠ECA=30°,∴∠BCE=∠EBC=60°.
AB.∴CE=AE,∴∠EAC=∠ECA=30°,∴∠BCE=∠EBC=60°.
又∵△AEF≌△BEC,∴∠AFE=∠BCE=60°.
又∵∠D=60°,∴∠AFE=∠D=60°.∴FC∥BD.
又∵∠BAD=∠ABC=60°,∴AD∥BC,即FD∥BC.∴四边形BCFD是平行四边形
(3)∵∠BAD=60°,∠CAB=30°,∴∠CAH=90°.
在Rt△ABC中,∠CAB=30°,BC=1,∴AB=2BC=2.∴AD=AB=2.
设AH=x,则HC=HD=AD﹣AH=2﹣x,在Rt△ABC中,AC2=22﹣12=3,
在Rt△ACH中,AH2+AC2=HC2,即x2+3=(2﹣x)2,解得x=![]() ,即AH=
,即AH=![]() .
.