题目内容
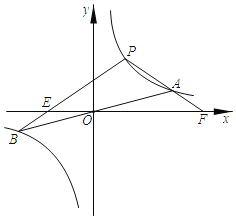
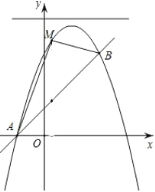
【题目】如图,在平面直角坐标系![]() 中,函数
中,函数![]() 的图象与直线
的图象与直线![]() 交于点
交于点![]() .M是函数
.M是函数![]() 图象上一点,过M作x轴的平行线交直线
图象上一点,过M作x轴的平行线交直线![]() 于点N.
于点N.
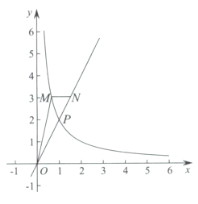
(1)求k和p的值;
(2)设点M的横坐标为m.
①求点N的坐标;(用含m的代数式表示)
②若![]() 的面积大于
的面积大于![]() ,结合图象直接写出m的取值范围.
,结合图象直接写出m的取值范围.
【答案】(1)![]() ,
,![]() ;(2)①
;(2)①![]() ;②
;②![]() 或者
或者![]() .
.
【解析】
(1)将点![]() 代入反比例函数的解析式可求出
代入反比例函数的解析式可求出![]() 的值,从而可得点P坐标,再将其代入直线
的值,从而可得点P坐标,再将其代入直线![]() 即可得出k的值;
即可得出k的值;
(2)①先根据反比例函数的解析式求出点M的纵坐标,从而可得点N的纵坐标,再将其代入直线的解析式可得点N的横坐标,从而可得出答案;
②分![]() 和
和![]() 两种情况,分别求出MN的长和MN边上的高,再根据三角形的面积公式列出不等式,求解即可得.
两种情况,分别求出MN的长和MN边上的高,再根据三角形的面积公式列出不等式,求解即可得.
(1)依题意,点![]() 在函数
在函数![]() 的图象上
的图象上
可得![]() ,则点
,则点![]()
将![]() 代入直线
代入直线![]() ,得
,得![]()
综上,![]() ,
,![]() ;
;
(2)①由于M是函数![]() 图象上一点,且点M的横坐标为m
图象上一点,且点M的横坐标为m
可得点M的纵坐标为![]()
则点![]()
又因为过M作x轴的平行线交直线![]() 于点N
于点N
则点N的纵坐标为![]()
当![]() 时,
时,![]() ,解得
,解得![]()
则点N的坐标为![]() ;
;
②由题意得:![]() 且
且![]() (因为当
(因为当![]() 时,点M、N重合,不能构成
时,点M、N重合,不能构成![]() )
)
因此,分以下两种情况:
(ⅰ)当![]() 时,
时,![]() ,边MN上的高为
,边MN上的高为![]()
则![]()
解得![]()
结合![]() 得:
得:![]()
(ⅱ)当![]() 时,
时,![]() ,边MN上的高为
,边MN上的高为![]()
则![]()
解得![]() (符合题设)或
(符合题设)或![]() (不符题设,舍去)
(不符题设,舍去)
综上,m的取值范围为![]() 或者
或者![]() .
.

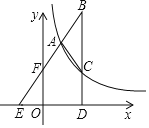
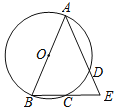
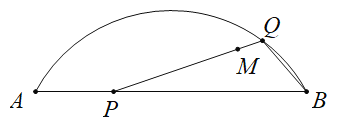
【题目】如图,M是弦![]() 与弧
与弧![]() 所围成的图形的内部的一个定点,P是弦
所围成的图形的内部的一个定点,P是弦![]() 上一动点,连接
上一动点,连接![]() 并延长交弧
并延长交弧![]() 于点Q,连接
于点Q,连接![]() .
.
已知![]() ,设A,P两点间的距离为
,设A,P两点间的距离为![]() ,P,Q两点间距离为
,P,Q两点间距离为![]() ,
,![]() 两点间距离为
两点间距离为![]() .
.
小明根据学习函数的经验,分别对函数![]() 随自变量x的变化而变化的规律进行了研究.下面是小明的探究过程,请补充完整.
随自变量x的变化而变化的规律进行了研究.下面是小明的探究过程,请补充完整.
(1)按照如表中自变量x的值进行取点、画图、测量,分别得到了![]() 与x的几组对应值,补全下表:
与x的几组对应值,补全下表:
| 0 | 1 | 2 | 3 | 4 | 5 | 6 |
| 5.24 | 4.24 | 3.24 | 1.54 | 1.79 | 3.47 | |
| 1.31 | 1.34 | 1.42 | 1.54 | 1.80 | 2.45 | 3.47 |
(2)在同一平面直角坐标系![]() 中,描出表中各组数值对应的点
中,描出表中各组数值对应的点![]() 和
和![]() 并画出函数
并画出函数![]() 的图象;
的图象;
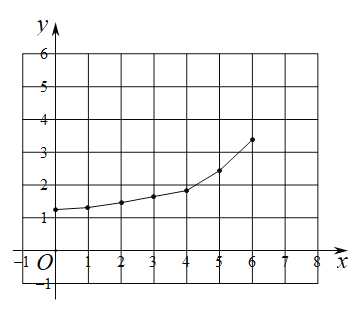
(3)结合函数图象,解决问题:当![]() 为等腰三角形时,
为等腰三角形时,![]() 的长度约_________
的长度约_________![]() .(精确到0.1)
.(精确到0.1)