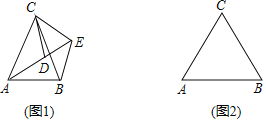题目内容
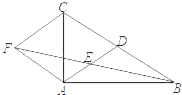
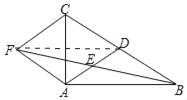
【题目】如图,在△ABC中,AD是BC边上的中线,点E是AD的中点,连接BE,过点A作BC的平行线交BE的延长线于点F,连接CF.
(1)求证:AF=DC;
(2)在不添加任何辅助线的情况下,请直接写出图中四个三角形,使写出的每个三角形的面积等于△AEF面积的2倍.
【答案】(1)见解析;(2)△ACF,△ACD,△ADB,△AFB.
【解析】
(1)根据平行线的性质可得∠AFE=∠DBE,然后利用AAS判定△AFE≌△DBE,可得AF=BD=CD;
(2)由题意可证四边形ADCF是平行四边形,四边形ABDF是平行四边形,即可求解.
证明:(1)证明:∵AF∥BC,
∴∠AFE=∠DBE,
∵E是AD的中点,
∴AE=DE,且∠AFE=∠DBE,∠AEF=∠DEB
∴△AFE≌△DBE(AAS);
∴AF=DB
∵AD是BC边上的中线,
∴DB=DC
∴AF=DC
(2)△ACF,△ACD,△ADB,△AFB
理由如下:连接DF
∵AF=CD,AF=DB,AF∥BC
∴四边形ADCF是平行四边形,四边形ABDF是平行四边形
∴S△ABF=2S△AEF=S△ABD=S△ACD=S△ACF,

 期末宝典单元检测分类复习卷系列答案
期末宝典单元检测分类复习卷系列答案【题目】我市某镇组织20辆汽车装运完![]() 三种品牌脐橙共100吨参加上海世博会,按计划,20辆汽车都要装运,每辆汽车只能装运用一种脐橙,且必须装满。根据下表提供的信息,解答以下问题:
三种品牌脐橙共100吨参加上海世博会,按计划,20辆汽车都要装运,每辆汽车只能装运用一种脐橙,且必须装满。根据下表提供的信息,解答以下问题:
从A,B两地运往甲,乙两地的费用如下表:
脐橙品种 | A | B | C |
每辆汽车运载量(吨) | 6 | 5 | 4 |
每吨脐橙获利(百元) | 12 | 16 | 10 |
(1)设装运![]() 种脐橙的车辆数为
种脐橙的车辆数为![]() ,装运
,装运![]() 种脐橙的车辆数为
种脐橙的车辆数为![]() ,求
,求![]() 与
与![]() 之间的函数关系式;
之间的函数关系式;
(2)如果装运每种脐橙的车辆数都不少于4辆,那么车辆的安排方案有几种?并写出每种安排方案?
(3)若要使此次销售获利最大,应采用哪种安排方案?请求出最大利润的值