Question

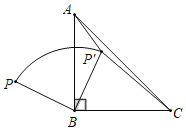
【题目】如图，点P是等腰Rt△ABC外一点，把线段BP绕点B顺时针旋转90°得到线段BP'，已知∠AP'B＝135°，P'A：P'C＝1：3，则P'A：PB＝_____．

Answer 1

【答案】

【解析】

连接AP和PP′，证明△ABP≌△CBP′，设P′A＝x，则AP＝3x，表示出BP，即可求出.

解：如图，连接AP和PP′，

∵BP绕点B顺时针旋转90°到BP′，

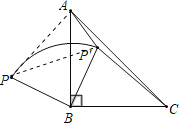
∴BP＝BP′，∠ABP+∠ABP′＝90°，

又∵△ABC是等腰直角三角形，

∴AB＝BC，∠CBP′+∠ABP′＝90°，

∴∠ABP＝∠CBP′，

在△ABP和△CBP′中，

，

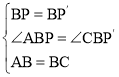∴△ABP≌△CBP′（SAS），

∴AP＝P′C，

∵P′A：P′C＝1：3，

∴AP＝3P′A，

∵△PBP′是等腰直角三角形，

∴∠BP′P＝45°，PP′＝PB，

∵∠AP′B＝135°，

∴∠AP′P＝135°﹣45°＝90°，

∴△APP′是直角三角形，

设P′A＝x，则AP＝3x，

根据勾股定理，PP′＝＝＝，

∴PP′＝PB＝，

解得PB＝2x，

∴P′A：PB＝x：2x＝1：2，

故答案为．