题目内容
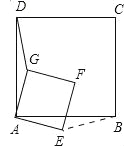
【题目】已知正方形ABCD和正方形AEFG有一个公共点A,点G、E分别在线段AD、AB上,若将正方形AEFG绕点A按顺时针方向旋转,连接DG,在旋转的过程中,你能否找到一条线段的长与线段DG的长度始终相等?并说明理由.

【答案】BE=DG,理由详见解析.
【解析】
试题分析:观察DG的位置,找包含DG的三角形,要使两条线段相等,只要找到与之全等的三角形,即可找到与之相等的线段.
试题解析:连接BE,则BE=DG.
理由如下:
∵四边形ABCD和四边形AEFG都是正方形,
∴AB=AD,AE=AG,∠BAD=∠EAG=90°,
∴∠BAD﹣∠BAG=∠EAG﹣∠BAG,即∠DAG=∠BAE,
则AB=AD,∠DAG=∠BAE,AE=AG,
∴△BAE≌△DAG(SAS),
∴BE=DG.

练习册系列答案
相关题目