Question

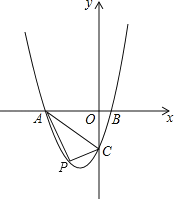
【题目】如图，正方形ABCD的对角线AC与BD相交于点O．将∠COB绕点O顺时针旋转，设旋转角为α（0＜α＜90°），角的两边分别与BC，AB交于点M，N，连接DM，CN，MN，下列四个结论：①∠CDM＝∠COM；②CN⊥DM；③△CNB≌△DMC；④AN2+CM2＝MN2；其中正确结论的个数是（　　）

A. 1B. 2C. 3D. 4

Answer 1

【答案】C

【解析】

利用正方形的性质进行等角转换，正方形ABCD的对角线AC与BD相交于点O，AC⊥BD，∠COM+∠MOB=∠BON+∠MOB=90°，∠COM=∠BON，OB=OC，∠OBN=∠OCM=45°，△ONB≌△OMC，得NB=MC，又BC=CD，∠DCM=∠CBN=90°，故△CNB≌△DMC

解：∵正方形ABCD的对角线AC与BD相交于点O

∴AC⊥BD，∠COM+∠MOB=∠BON+∠MOB=90°

∴∠COM=∠BON，OB=OC，∠OBN=∠OCM=45°

∴△ONB≌△OMC

∴NB=MC

又∵BC=CD，∠DCM=∠CBN=90°

∴△CNB≌△DMC

∴③结论正确；

由△CNB≌△DMC，得出∠BCN=∠CDM

又∠CDM+∠CMD=90°

∴∠BCN+∠CMD=90°

∴CN⊥DM

故②结论正确.