题目内容
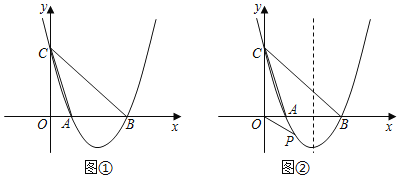
【题目】已知△ABC中,∠ACB=90°,将AB边绕点B顺时针旋转90°得线段BD.过点D作DM⊥BC交BC延长线于M,
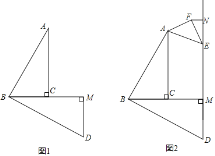
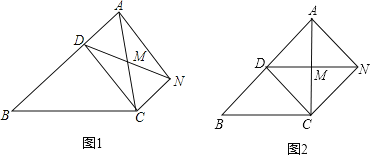
(1)如图1,请判断线段AC、CM、MD的数量关系并说明理由;
(2)E为DM延长线上一点,当点E为如图2所示的位置时,以AE为斜边向右侧作等腰Rt△AFE,再过点F作FN⊥DM于N,探究BM、FN、MN三条线段的数量关系,并说明理由;
(3)在问题(2)的条件下,当点E运动到某一位置时点B、A、F三点恰好在同一直线上,取DE中点P,连接AP,且AB=3,AF=1,请直接写出AP的值.
【答案】(1)AC=MD+MC,理由见解析;(2)MN=FN+BM,理由见解析;(3)![]()
【解析】
(1)由旋转的性质可得AB=BD,∠ABD=90°,由“AAS”可证△ABC≌△BDM,可得AC=BM,BC=MD,可证AC=MD+MC;
(2)如图2,延长NF,CA交于点H,可证四边形HCMN是矩形,可得MN=HC,∠H=90°,由“AAS”可证△AFH≌△FEN,可得AH=FN,可得结论;
(3)如图3,过点A作AG⊥MN,由相似三角形的性质可得BC=3HF,AC=3AH,由勾股定理可求HF、AH、PE,再利用勾股定理即可求得答案.
(1)AC=MD+MC,
理由如下:
∵将AB边绕点B顺时针旋转90°得线段BD,
∴AB=BD,∠ABD=90°,
∴∠ACB=∠ABD=90°,
∴∠A+∠ABC=90°,∠ABC+∠DBM=90°,
∴∠A=∠DBM,
在△ABC和△BDM中,
 ,
,
∴△ABC≌△BDM(AAS)
∴AC=BM,BC=MD,
∵BM=BC+CM,
∴AC=MD+MC;
(2)MN=FN+BM,
理由如下:
如图2,延长NF,CA交于点H,
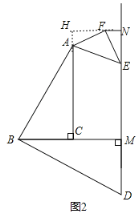
∵∠ACM=∠BMN=90°,FN⊥MN,
∴四边形HCMN是矩形,
∴MN=HC,∠H=90°,HN=CM,
∵△AEF是等腰直角三角形,
∴AF=EF,∠AFE=90°=∠H,
∴∠HFA+∠HAF=90°,∠HFA+∠NFE=90°,
∴∠NFE=∠HAF,
在△AFH和△FEN中,
 ,
,
∴△AFH≌△FEN(AAS)
∴AH=FN,
∵MN=HC=AC+AH,
∴MN=FN+BM;
(3)如图3,延长NF,CA交于点H,过点A作AG⊥MN,

∵∠ACM=∠BMN=90°,FN⊥MN,AG⊥MN,
∴四边形HCMN、ACMG、AGNH是矩形,
∴AG=HN,AH=NG,MN=CH,
∵FN⊥MN,DM⊥BC,
∴NH∥BM,
∴△ABC∽△AFH,
∴![]() ,
,
∴BC=3HF,AC=3AH,
由(2)得:CM=HN,AH=FN,FH=EN,AC=BM,
∴AC﹣BC= BM﹣BC=CM=HN=FH+FN,
∴3AH﹣3HF=HF+AH,
∴AH=2HF,
∵AH2+HF2=AF2=1,
∴HF=![]() ,AH=
,AH=![]() ,
,
∴HN=![]() ,BC=
,BC=![]() =MD,AC=
=MD,AC=![]() ,MN=CH= AC+ AH=
,MN=CH= AC+ AH=![]() ,
,
∴DE=MD+MN﹣NE=![]() ,
,
∵点P是DE中点,
∴PE=![]() ,
,
∴AG=HN=![]() ,AH=NG=
,AH=NG=![]() ,
,
∴EG= NG- EN= NG- HF=![]() ,
,
∴GP=EP﹣EG=![]() ,
,
∴ .
.