题目内容
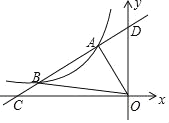
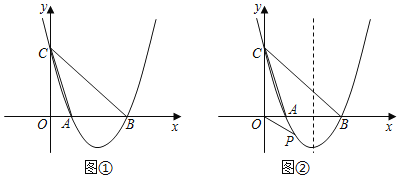
【题目】如图①,已知抛物线y=ax2﹣4amx+3am2(a、m为参数,且a>0,m>0)与x轴交于A、B两点(A在B的左边),与y轴交于点C.
(1)求点B的坐标(结果可以含参数m);
(2)连接CA、CB,若C(0,3m),求tan∠ACB的值;
(3)如图②,在(2)的条件下,抛物线的对称轴为直线l:x=2,点P是抛物线上的一个动点,F是抛物线的对称轴l上的一点,在抛物线上是否存在点P,使△POF成为以点P为直角顶点的的等腰直角三角形.若存在,求出所有符合条件的点P的坐标,若不存在,请说明理由.
【答案】(1)B(3m,0);(2)tan∠ACB=![]() ;
;
(3)点P的坐标是:(![]() )或(
)或(![]() )或(
)或(![]() )或(
)或(![]() ).
).
【解析】
(1)令y=0,解方程ax2﹣4amx+3am2=0,即可求出点B的坐标;
(2)过点A作AD⊥BC,垂足为点D,可得△BOC为等腰直角三角形,求出AD,CD,则tan∠ACB的值为![]() ;
;
(3)求出抛物线的解析式,分不同的情况:①当P在对称轴的左边,如图3,过P作MN⊥y轴,交y轴于M,交l于N,证明△OMP≌△PNF,根据|OM|=|PN|,列方程可得点P的坐标;同理可得其他图形中点P的坐标,②当P在对称轴的左边,过P作MN⊥x轴于N,过F作FM⊥MN于M,同理得△ONP≌△PMF,则可求出点P的坐标.
解:(1)令y=0,则有ax2﹣4amx+3am2=0,
解得:x1=m,x2=3m,
∵m>0,A在B的左边,
∴B(3m,0);
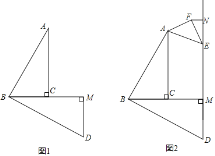
(2)如图1,过点A作AD⊥BC,垂足为点D,
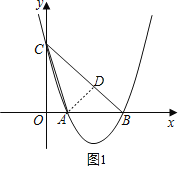
由(1)可知B(3m,0),则△BOC为等腰直角三角形,
∵OC=OB=3m,
∴BC=3![]() m,
m,
又∵∠ABC=45°,
∴∠DAB=45°,
∴AD=BD,
∵AB=2m,
∴![]() m,CD=2
m,CD=2![]() m,
m,
∴tan∠ACB=![]() ;
;
(3)∵由题意知x=2为对称轴,
∴2m=2,
即m=1,
∵在(2)的条件下有(0,3m),
∴3m=3am2,
解得m=![]() ,即a=1,
,即a=1,
∴抛物线的解析式为y=x2﹣4x+3,
①当P在对称轴的左边,如图2,过P作MN⊥y轴,交y轴于M,交l于N,
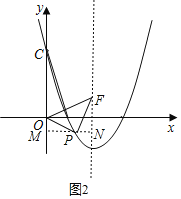
∵△OPF是等腰直角三角形,且OP=PF,
易得△OMP≌△PNF,
∴OM=PN,
∵P(m,m2﹣4m+3),
则﹣m2+4m﹣3=2﹣m,
解得:m=![]() 或
或![]() ,
,
∴P的坐标为(![]() ,
,![]() )或(
)或(![]() );
);
②当P在对称轴的右边,
如图3,过P作MN⊥x轴于N,过F作FM⊥MN于M,

同理得△ONP≌△PMF,
∴PN=FM,
则﹣m2+4m﹣3=m﹣2,
解得:x=![]() 或
或![]() ;
;
P的坐标为(![]() )或(
)或(![]() );
);
综上所述,点P的坐标是:(![]() )或(
)或(![]() )或(
)或(![]() )或(
)或(![]() ).
).

 名校课堂系列答案
名校课堂系列答案