题目内容
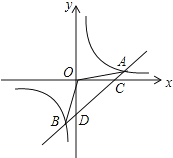
【题目】如图,一次函数y=x+b和反比例函数y=![]() (k≠0)交于点A(4,1).
(k≠0)交于点A(4,1).
(1)求反比例函数和一次函数的解析式;
(2)求△AOB的面积;
(3)根据图象直接写出一次函数的值大于反比例函数的值的x的取值范围.
【答案】(1)反比例函数的解析式为:y=![]() ;一次函数的解析式为:y=x﹣3;
;一次函数的解析式为:y=x﹣3;
(2)S△AOB=![]() ;
;
(3)一次函数的值大于反比例函数的值的x的取值范围为:﹣1<x<0或x>4.
【解析】
(1)把A的坐标代入y=![]() ,求出反比例函数的解析式,把A的坐标代入y=x+b求出一次函数的解析式;
,求出反比例函数的解析式,把A的坐标代入y=x+b求出一次函数的解析式;
(2)求出D、B的坐标,利用S△AOB=S△AOD+S△BOD计算,即可求出答案;
(3)根据函数的图象和A、B的坐标即可得出答案.
(1)∵反比例函数y=![]() 的图象过点A(4,1),
的图象过点A(4,1),
∴1=![]() ,即k=4,
,即k=4,
∴反比例函数的解析式为:y=![]() .
.
∵一次函数y=x+b(k≠0)的图象过点A(4,1),
∴1=4+b,解得b=﹣3,
∴一次函数的解析式为:y=x﹣3;
(2)∵令x=0,则y=﹣3,
∴D(0,﹣3),即DO=3.
解方程![]() =x﹣3,得x=﹣1,
=x﹣3,得x=﹣1,
∴B(﹣1,﹣4),
∴S△AOB=S△AOD+S△BOD=![]() ×3×4+
×3×4+![]() ×3×1=
×3×1=![]() ;
;
(3)∵A(4,1),B(﹣1,﹣4),
∴一次函数的值大于反比例函数的值的x的取值范围为:﹣1<x<0或x>4.

 鸿图图书寒假作业假期作业吉林大学出版社系列答案
鸿图图书寒假作业假期作业吉林大学出版社系列答案【题目】庐阳春风体育运动品商店从厂家购进甲,乙两种T恤共400件,其每件的售价与进货量![]() (件)之间的关系及成本如下表所示:
(件)之间的关系及成本如下表所示:
T恤 | 每件的售价/元 | 每件的成本/元 |
甲 |
| 50 |
乙 |
| 60 |
|
(1)当甲种T恤进货250件时,求两种T恤全部售完的利润是多少元;
(2)若所有的T恤都能售完,求该商店获得的总利润![]() (元)与乙种T恤的进货量
(元)与乙种T恤的进货量![]() (件)之间的函数关系式;
(件)之间的函数关系式;
(3)在(2)的条件下,已知两种T恤进货量都不低于100件,且所进的T恤全部售完,该商店如何安排进货才能使获得的利润最大?
【题目】某塑料厂生产一种家用塑料制品,它的成本是![]() 元
元![]() 件,售价是
件,售价是![]() 元
元![]() 件,年销售量为
件,年销售量为![]() 万件.为了获得更好的效益,厂家准备拿出一定的资金做广告.根据测算,若每年投入广告费
万件.为了获得更好的效益,厂家准备拿出一定的资金做广告.根据测算,若每年投入广告费![]() 万元,产品的年销售量将是原销售量的
万元,产品的年销售量将是原销售量的![]() 倍,且
倍,且![]() 与
与![]() 之间满足
之间满足![]() ,具体数量如下表:
,具体数量如下表:
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(1)求![]() 与
与![]() 的函数关系式(不要求写出自变量的取值范围);
的函数关系式(不要求写出自变量的取值范围);
(2)如果把利润看作是销售总额减去成本费用和广告费用,试求出年利润![]() (万元)与广告费用
(万元)与广告费用![]() (万元)的函数关系式,并计算每年投入的广告费是多少万元时,所获得的利润最大?
(万元)的函数关系式,并计算每年投入的广告费是多少万元时,所获得的利润最大?
(3)如果厂家希望年利润![]() (万元)不低于
(万元)不低于![]() 万元,请你帮助厂家确定广告费
万元,请你帮助厂家确定广告费![]() 的范围.
的范围.