题目内容
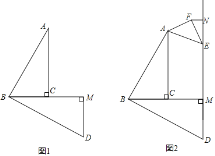
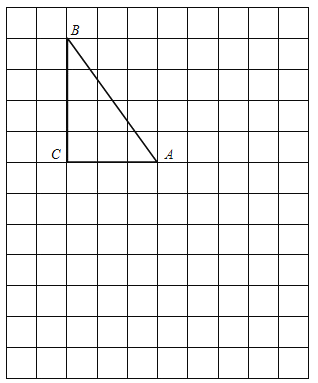
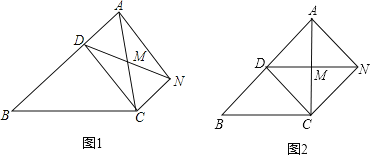
【题目】已知,如图1,D是△ABC的边上一点,CN∥AB,DN交AC于点M,MA=MC.
(1)求证:四边形ADCN是平行四边形.
(2)如图2,若∠AMD=2∠MCD,∠ACB=90°,AC=BC.请写出图中所有与线段AN相等的线段(线段AN除外)
【答案】(1)证明见解析;(2)AN=AD=BD=CD=CN.
【解析】
(1)由CN∥AB,MA=MC,易证得△AMD≌△CMN,则可得MD=MN,即可证得四边形ADCN是平行四边形.
(2)由∠AMD=2∠MCD,可证得四边形ADCN是矩形,又由∠ACB=90°,AC=BC,可得四边形ADCN是正方形,继而求得答案.
(1)证明:∵CN∥AB,
∴∠DAM=∠NCM,
在△ADM和△CNM中,
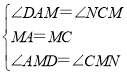 ,
,
∴△AMD≌△CMN(ASA),
∴MD=MN,
又MA=MC,
∴四边形ADCN是平行四边形.
(2)解:∵∠AMD=2∠MCD,∠AMD=∠MCD+∠MDC,
∴∠MCD=∠MDC,
∴MC=MD,
∴AC=DN,
∴ADCN是矩形,
∵AC=BC,
∴AD=BD,
∵∠ACB=90°,
∴CD=AD=BD=![]() AB,
AB,
∴ADCN是正方形,
∴AN=AD=BD=CD=CN.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
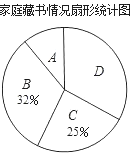
【题目】在“书香校园”活动中,某校为了解学生家庭藏书情况,随机抽取本校部分学生进行调查,并绘制成部分统计图表如下:
类别 | 家庭藏书m本 | 学生人数 |
A | 0≤m≤25 | 20 |
B | 26≤m≤100 | a |
C | 101≤m≤200 | 50 |
D | m≥201 | 66 |
根据以上信息,解答下列问题:
(1)该调查的样本容量为_____,a=_____;
(2)在扇形统计图中,“A”对应扇形的圆心角为_____°;
(3)若该校有2000名学生,请估计全校学生中家庭藏书200本以上的人数.