题目内容
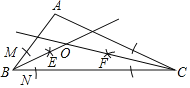
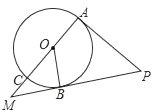
【题目】如图,AC是⊙O的直径,OB是⊙O的半径,PA切⊙O于点A,PB与AC的延长线交于点M,∠COB=∠APB.
(1)求证:PB是⊙O的切线;
(2)当MB=4,MC=2时,求⊙O的半径.
【答案】(1)证明见解析;(2)3.
【解析】
(1)根据题意∠M+∠P=90°,而∠COB=∠APB,所以有∠M+∠COB=90°,即可证明PB是⊙O的切线.
(2)设圆的半径为r,则OM=r+2,BM=4,OB=r,再根据勾股定理列方程便可求出r.
证明:(1)∵AC是⊙O的直径,PA切⊙O于点A,
∴PA⊥OA
∴在Rt△MAP中,∠M+∠P=90°,而∠COB=∠APB,
∴∠M+∠COB=90°,
∴∠OBM=90°,即OB⊥BP,
∴PB是⊙O的切线;
(2)设⊙O的半径为r,
![]() ,
,![]() ,
,![]()
![]() 为直角三角形
为直角三角形
∴![]() ,即
,即![]()
解得:r=3,
∴⊙O的半径为3.

练习册系列答案
 阳光考场单元测试卷系列答案
阳光考场单元测试卷系列答案 名校联盟冲刺卷系列答案
名校联盟冲刺卷系列答案 名校提分一卷通系列答案
名校提分一卷通系列答案 课程达标测试卷闯关100分系列答案
课程达标测试卷闯关100分系列答案
相关题目