题目内容
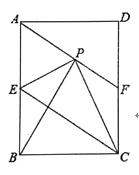
【题目】如图①,在![]() 中,∠C=90°,AC=3,BC=4.求作菱形DEFG,使点D在边AC上,点E、F在边AB上,点G在边BC上.
中,∠C=90°,AC=3,BC=4.求作菱形DEFG,使点D在边AC上,点E、F在边AB上,点G在边BC上.
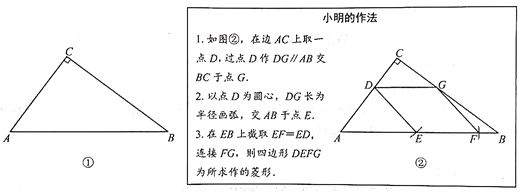
(1)证明小明所作的四边形DEFG是菱形;
(2)小明进一步探索,发现可作出的菱形的个数随着点D的位置变化而变化……请你继续探索,直接写出菱形的个数及对应的CD的长的取值范围.
【答案】(1)见解析;(2)菱形的个数为2,![]() .
.
【解析】
(1)根据邻边相等的四边形是菱形证明即可.
(2)求出几种特殊位置的CD的值判断即可.
解:(1)证明:∵![]() ,
,
∴![]() .
.
又![]() ,
,
∴四边形![]() 是平行四边形.
是平行四边形.
又![]() ,
,
∴![]() 是菱形.
是菱形.
(2)如图1中,当四边形DEFG是正方形时,设正方形的边长为x.
在Rt△ABC中,∵∠C=90°,AC=3,BC=4,
∴AB=![]() ,
,
则CD=![]() x,AD=
x,AD=![]() x,
x,
∵AD+CD=AC,
∴![]() x+
x+![]() x=3,
x=3,
∴x=![]() ,
,
∴CD=![]() x=
x=![]() ,
,
观察图象可知:0≤CD<![]() 时,菱形的个数为0.
时,菱形的个数为0.
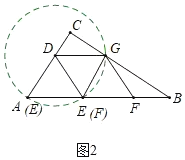
如图2中,当四边形DAEG是菱形时,设菱形的边长为m.
∵DG∥AB,
∴![]() ,,
,,
∴![]() ,
,
解得m=![]() ,
,
∴CD=3![]() ,
,
如图3中,当四边形DEBG是菱形时,设菱形的边长为n.
∵DG∥AB,
∴![]() ,
,
∴![]() ,
,
∴n=![]() ,
,
∴CG=4![]() ,
,
∴CD= ,
,
观察图象可知:
当![]() 或
或![]() 时,菱形的个数为0;
时,菱形的个数为0;
当![]() 或
或![]() 时,菱形的个数为1;
时,菱形的个数为1;
当![]() 时,菱形的个数为2.
时,菱形的个数为2.



练习册系列答案
相关题目