题目内容
【题目】已知二次函数y=ax2+bx+c的图象C经过(﹣5,0),(0, ![]() ),(1,6)三点,直线l的解析式为y=2x﹣3.
),(1,6)三点,直线l的解析式为y=2x﹣3.
(1)求抛物线C的解析式;
(2)判断抛物线C与直线l有无交点;
(3)若与直线l平行的直线y=2x+m与抛物线C只有一个公共点P,求点P的坐标.
【答案】
(1)解:∵二次函数y=ax2+bx+c的图象抛物线C经过(﹣5,0),(0, ![]() ),(1,6)三点,
),(1,6)三点,
∴ 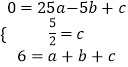 ,解得
,解得 ![]() ,
,
∴抛物线C的函数解析式为:y= ![]() x2+3x+
x2+3x+ ![]()
(2)解:∵由(1)得抛物线C的函数解析式为:y= ![]() x2+3x+
x2+3x+ ![]() ,
,
∴代入y=2x﹣3得2x﹣3=x2+3x+ ![]() ,
,
整理得 ![]() x2+x+
x2+x+ ![]() =0,
=0,
∵△=12﹣4× ![]() ×
× ![]() =﹣10<0,
=﹣10<0,
∴方程无实数根,即抛物线C与直线l无公共点
(3)解:∵与l平行的直线y=2x+m与抛物线G只有一个公共点P,
∴ 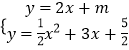 ,消去y得,
,消去y得, ![]() x2+x+
x2+x+ ![]() ﹣m=0①,
﹣m=0①,
∵抛物线C与直线y=2x+m只有一个公共点P,
∴△=12﹣4× ![]() ×(
×( ![]() ﹣m)=0,解得m=2,
﹣m)=0,解得m=2,
把m=2代入方程①得, ![]() x2+x+
x2+x+ ![]() ﹣2=0,解得x=﹣1,
﹣2=0,解得x=﹣1,
把x=﹣1代入直线y=2x+2得,y=0,
∴P(﹣1,0).
【解析】(1)直接把点(﹣5,0),(0, ![]() ),(1,6)代入二次函数y=ax2+bx+c,求出a、b、c的值即可;(2)把(1)中求出的抛物线的解析式与直线l的解析式y=2x﹣3组成方程组,再根据一元二次方程根的判别式即可得出结论;(3)把直线y=2x+m与抛物线C的解析式组成方程组,根据只有一个公共点P可知△=0,求出m的值,故可得出P点坐标即可.
),(1,6)代入二次函数y=ax2+bx+c,求出a、b、c的值即可;(2)把(1)中求出的抛物线的解析式与直线l的解析式y=2x﹣3组成方程组,再根据一元二次方程根的判别式即可得出结论;(3)把直线y=2x+m与抛物线C的解析式组成方程组,根据只有一个公共点P可知△=0,求出m的值,故可得出P点坐标即可.

练习册系列答案
相关题目