题目内容
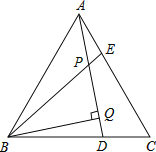
【题目】如图,△ABC为等边三角形,AE=CD,AD、BE相交于点P,BQ⊥AD于Q.
(1)求证:△ADC≌△BEA;
(2)若PQ=4,PE=1,求AD的长.
【答案】(1)证明见解析;(2)9.
【解析】
试题(1)由已知可得△ABC是等边三角形,从而得到∠BAC=∠C=60°,根据SAS即可判定△ADC≌△BEA;
(2)根据全等三角形的性质可得到∠ABE=∠CAD,再根据等角的性质即可求得∠BPQ=60°,再根据余角的性质得到∠PBQ=30°,根据在直角三角形中30°的角对的边是斜边的一半即可证得结果.
试题解析:(1)∵AB=BC=AC,
∴△ABC是等边三角形.
∴∠BAC=∠C=60°.
∵AB=AC,AE=CD,
∴△ADC≌△BEA.
(2)∵△ADC≌△BEA,
∴∠ABE=∠CAD.
∵∠CAD+∠BAD=60°,
∴∠ABE+∠BAD=60°.
∴∠BPQ=60°.
∵BQ⊥AD,
∴∠PBQ=30°.
∴BP=2PQ=8.
∴BE=BP+PE=8+1=9,
又BE=AD
∴AD=9.
考点: 1.等边三角形的判定与性质;2.三角形全等的判定与性质.

练习册系列答案
相关题目