题目内容
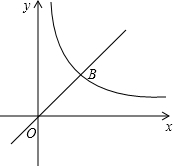
如图,已知双曲线y=
与直线y=kx+b交于第一象限点P(2,3),且直线穿过点A(0,2)
(1)求两个函数的解析式;
(2)若直线与x轴交于点B,求S△BOP的值.

| m |
| x |
(1)求两个函数的解析式;
(2)若直线与x轴交于点B,求S△BOP的值.

解;(1)∵双曲线y=
与直线y=kx+b交于第一象限点P(2,3),且直线穿过点A(0,2),
∴m=2×3=6,
,
解得:
.
∴直线解析式为:y=
x+2,双曲线解析式为:y=
;
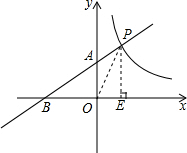
(2)连接OP,作PE⊥x轴于点E,
∵y=
x+2=0时,x=-4,
∴直线与x轴交于点(-4,0),
∴BO=4,
∵点P(2,3),
∴PE的长为:3,
∴S△BOP=
×BO×PE=
×4×3=6.
| m |
| x |
∴m=2×3=6,
|
解得:
|
∴直线解析式为:y=
| 1 |
| 2 |
| 6 |
| x |
(2)连接OP,作PE⊥x轴于点E,
∵y=
| 1 |
| 2 |
∴直线与x轴交于点(-4,0),
∴BO=4,
∵点P(2,3),
∴PE的长为:3,
∴S△BOP=
| 1 |
| 2 |
| 1 |
| 2 |


练习册系列答案
相关题目