题目内容
【题目】如图，
是
的角平分线，
、
分别是边
、
的中点，连接
、
，在不再连接其他线段的前提下，要使四边形
成为菱形，还需添加一个条件，这个条件不可能是（ ）
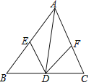
A. BD=DC B. AB=AC
C. AD=BC D. AD⊥BC
【答案】C
【解析】
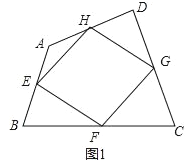
可以添加BD=CD或AB=AC或AD⊥BC，然后利用三角形中位线证明四边形ADEF是平行四边形，再证明是菱形即可．
添加BD=CD，
∵E、F分别是边AB、AC的中点，
∴DE，EF是三角形的中位线，
∴DE∥AB，DF∥AC，
∴四边形ADEF是平行四边形，
∵AB=AC，
点E，F分别是AB，AC的中点，
∴AE=AF，
∴平行四边形ADEF为菱形．
添加AB=AC，则三角形是等腰三角形，
由等腰三角形的性质知，顶角的平分线与底边上的中线重合，
即点D是BC的中点再证明即可；
添加AD⊥BC，
再由AD是△ABC的角平分线可证明△ABD≌△ACD，进而得到BD=CD，再证明四边形ADEF为菱形即可，
故选C．
练习册系列答案
相关题目
