题目内容
热气球C从建筑物A的底部沿直线开始斜着往上飞行,当飞行了180米距离时到达如图中的位置,此时在热气球上测得两建筑物A,B底部的俯角分别为30°和60°﹒若此时热气球在地面的正投影D与点A,B在同一直线上.
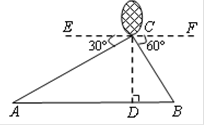
(1)求此时热气球离地面的高度CD的长;
(2)求建筑物A、B之间的距离(结果中保留根号).

(1)求此时热气球离地面的高度CD的长;
(2)求建筑物A、B之间的距离(结果中保留根号).
(1)CD=90米;(2)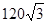 米.
米.
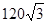 米.
米.试题分析:(1)由题意知,∠A=30°,AC=180米,∠ADC=90°,根据正弦函数的定义sin∠A=
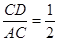 ,即可求得CD=90米.(2)在Rt△ACD中,根据正切函数的定义tan∠A=
,即可求得CD=90米.(2)在Rt△ACD中,根据正切函数的定义tan∠A=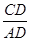 ,可求出AD的长度,同理在Rt△BCD中,根据正切函数定义tan∠B=
,可求出AD的长度,同理在Rt△BCD中,根据正切函数定义tan∠B=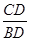 ,可求出BD的长度,从而可求出AB的长度.归纳:遇到解直角三角形的问题时,通常把要求的线段或角放在直角三角形中,利用三角函数的定义来求,如果没有直角三角形,可通过添加辅助线,构造直角三角形.
,可求出BD的长度,从而可求出AB的长度.归纳:遇到解直角三角形的问题时,通常把要求的线段或角放在直角三角形中,利用三角函数的定义来求,如果没有直角三角形,可通过添加辅助线,构造直角三角形.试题解析:(1)由题意可知EF∥AB,
∴∠A=∠ECA=30°,
∵AC=180m,
∴CD=90米,
答:热气球离地面的高度CD的长是90米;
(2)解:在直角△ACD中,∠A=30°,tanA=
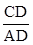 =
=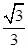 ,
,∴AD=
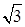 CD=90
CD=90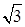 ,同理,BD=
,同理,BD=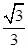 CD=30
CD=30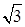 ,
,则AB=AD+BD=120
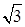 (米)
(米)答:建筑物A,B之间的距离是120
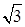 米.
米. 
练习册系列答案
 优等生题库系列答案
优等生题库系列答案 53天天练系列答案
53天天练系列答案
相关题目
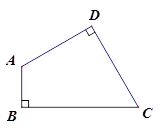
 .
. ,求锐角α.
,求锐角α.


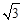 m
m m
m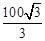 m
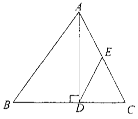
m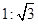 ,坡顶的平地BC上有一棵小树AB,当太阳光线与水平线夹角成60°时,测得小树的在坡顶平地上的树影BC是3米,斜坡上的树影CD是
,坡顶的平地BC上有一棵小树AB,当太阳光线与水平线夹角成60°时,测得小树的在坡顶平地上的树影BC是3米,斜坡上的树影CD是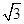 米,则小树AB的高是 米.
米,则小树AB的高是 米.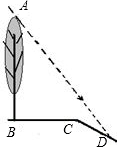
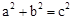 ,那么下列结
,那么下列结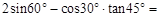 ____________
____________