题目内容
【题目】在四边形ABCD中,AD∥BC,DE平分∠ADB,∠BDC=∠C.若∠ABD的平分线与CD的延长线交于F,且∠F=x°(其中0<x<90),则∠ABC=°,(用含有x的式子表示) 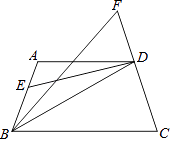
【答案】(180﹣2x)
【解析】解:如图, 
∵AD∥BC,
∴∠ADF=∠C=∠BDC,
∵∠EDA=∠EDB,
∴∠ADF+∠EDA=90°,即∠EDF=90°
∴∠3=90°﹣x,
∵∠3=∠1+∠2= ![]() (∠ABD+∠ADB)=
(∠ABD+∠ADB)= ![]() (180°﹣∠A)=90°﹣
(180°﹣∠A)=90°﹣ ![]() ∠A,
∠A,
∴90°﹣x=90°﹣ ![]() ∠A,
∠A,
∴∠A=2x,
∵∠A+∠ABC=180°,
∴∠ABC=180°﹣2x.
所以答案是180﹣2x.
【考点精析】关于本题考查的平行线的性质和多边形内角与外角,需要了解两直线平行,同位角相等;两直线平行,内错角相等;两直线平行,同旁内角互补;多边形的内角和定理:n边形的内角和等于(n-2)180°.多边形的外角和定理:任意多边形的外角和等于360°才能得出正确答案.

练习册系列答案
相关题目