题目内容
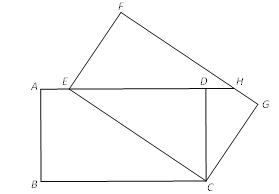
【题目】如图,矩形AEFG的顶点E,G分别在正方形ABCD的AB,AD边上,连接B,交EF于点M,交FG于点N,设AE=a,AG=b,AB=c(b<a<c).
(1)求证: ![]() ;
;
(2)求△AMN的面积(用a,b,c的代数式表示);
(3)当∠MAN=45°时,求证:c2=2ab.

【答案】(1)证明见解析;(2)![]() c(a+b﹣c);(3)证明见解析.
c(a+b﹣c);(3)证明见解析.
【解析】试题分析:(1)首先过点N作NH⊥AB于点H,过点M作MI⊥AD于点I,可得△NHB和△DIM是等腰直角三角形,四边形AGNH和四边形AEMI是矩形,则可求得BN=![]() b,DM=
b,DM=![]() a,继而求得答案;
a,继而求得答案;
(2)由S△AMN=S△ABD-S△ABM-S△ADN,可得S△AMN=![]() c2-
c2-![]() c(c-a)-
c(c-a)-![]() c(c-b),继而求得答案;
c(c-b),继而求得答案;
(3)易证得∴∠DMA=∠BAN,又由∠ABD=∠ADB=45°,可证得△ADM∽△NBA,然后由相似三角形的对应边成比例,求得答案.
试题解析:(1)证明:过点N作NH⊥AB于点H,过点M作MI⊥AD于点I,
∵四边形ABCD是正方形,
∴∠ADB=∠ABD=45°,
∴△NHB和△DIM是等腰直角三角形,四边形AGNH和四边形AEMI是矩形,
∴BN=![]() NH=
NH=![]() AG=
AG=![]() b,DM=
b,DM=![]() MI=
MI=![]() AE=
AE=![]() a,
a,
∴![]() ;
;
(2)S△AMN=S△ABD﹣S△ABM﹣S△ADN
=![]() ABAD﹣
ABAD﹣![]() ABME﹣
ABME﹣![]() ADNG
ADNG
=![]() c2﹣
c2﹣![]() c(c﹣a)﹣
c(c﹣a)﹣![]() c(c﹣b)
c(c﹣b)
=![]() c(c﹣c+a﹣c+b)
c(c﹣c+a﹣c+b)
=![]() c(a+b﹣c);
c(a+b﹣c);
(3)∵∠DMA=∠ABD+∠MAB=∠MAB+45°,∠BAN=∠MAB+∠MAN=∠MAB+45°,
∴∠DMA=∠BAN,
∵∠ABD=∠ADB=45°,
∴△ADM∽△NBA,
∴![]() ,
,
∵DM=![]() a,BN=
a,BN=![]() b,
b,
∴c2=2ab.


练习册系列答案
 口算题卡北京妇女儿童出版社系列答案
口算题卡北京妇女儿童出版社系列答案
相关题目