题目内容
【题目】如图,四边形ABCD中,对角线AC,BD相交于点O,点E,F分别在线段OA,OC上,且OB=OD,∠1=∠2,AE=CF.
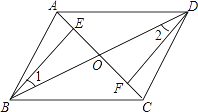
(1)证明:△BEO≌△DFO;
(2)证明:四边形ABCD是平行四边形.
【答案】(1)证明见解析;(2)证明见解析.
【解析】试题分析:(1)由条件可利用ASA证得结论;
(2)由(1)的结合可得OE=OF,则可求得AE=CF,可求得OA=OC,则可证得四边形ABCD为平行四边形.
试题解析:(1)证明:∵∠EOB与∠FOD是对顶角,
∴∠EOB=∠FOD,
在△BEO和△DFO中
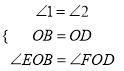 ,
,
∴△BEO≌△DFO(ASA)
(2)证明:由(1)可知△BEO≌△DFO,
∴OE=OF,
∵AE=CF,
∴OA=OC,
∵OB=OD,
∴四边形ABCD为平行四边形.

练习册系列答案
 怎样学好牛津英语系列答案
怎样学好牛津英语系列答案
相关题目