题目内容
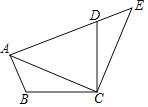
【题目】在△ABC中,∠BAC=100°,∠ABC=∠ACB,点D在直线BC上运动(不与点B、C重合),点E在射线AC上运动,且∠ADE=∠AED,设∠DAC=n.
(1)如图(1),当点D在边BC上时,且n=36°,则∠BAD= _________,∠CDE= _________.
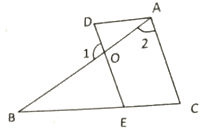
(2)如图(2),当点D运动到点B的左侧时,其他条件不变,请猜想∠BAD和∠CDE的数量关系,并说明理由.
(3)当点D运动到点C的右侧时,其他条件不变,∠BAD和∠CDE还满足(2)中的数量关系吗?请画出图形,并说明理由.

【答案】64° 32°
【解析】
(1)由∠BAC=100°,可求出∠ABC=∠ACB=40°,当∠DAC=36°时,根据∠BAD=∠BAC-∠DAC可求出∠BAD的度数,根据等腰三角形的性质求出∠ADE=∠AED的度数,再根据三角形的外角的性质求解.
(2) 由思路(1)可知∠ABC=∠ACB=40°,以及∠ADE=∠AED=![]() ,∠CDE=∠ACB-∠AED,∠BAD=n-100°,即可求解.
,∠CDE=∠ACB-∠AED,∠BAD=n-100°,即可求解.
(3)根据(1)的思路,可知∠ABC=∠ACB=40°,∠ADE=∠AED=![]() ,∠CDE=∠ACD-∠AED,∠BAD=100°+n,即可求解.
,∠CDE=∠ACD-∠AED,∠BAD=100°+n,即可求解.
(1)∠BAD=∠BAC-∠DAC=100°-36°=64°.
∵在△ABC中,∠BAC=100°,∠ABC=∠ACB,
∴∠ABC=∠ACB=40°,
∴∠ADC=∠ABC+∠BAD=40°+64°=104°.
∵∠DAC=36°,∠ADE=∠AED,
∴∠ADE=∠AED=72°,
∴∠CDE=∠ADC-∠ADE=104°-72°=32°.
故答案为64°,32°.
(2)∠BAD=2∠CDE,理由如下:
如图(2),在△ABC中,∠BAC=100°,
∴∠ABC=∠ACB=40°.
在△ADE中,∠DAC=n,
∴∠ADE=∠AED=![]() .
.
∵∠ACB=∠CDE+∠AED,
∴∠CDE=∠ACB-∠AED=40°-![]() =
=![]() .
.
∵∠BAC=100°,∠DAC=n,
∴∠BAD=n-100°,
∴∠BAD=2∠CDE;
(3)∠BAD=2∠CDE,理由如下:
如图(3),在△ABC中,∠BAC=100°,
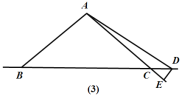
∴∠ABC=∠ACB=40°,
∴∠ACD=140°.
在△ADE中,∠DAC=n,
∴∠ADE=∠AED=![]() .
.
∵∠ACD=∠CDE+∠AED,
∴∠CDE=∠ACD-∠AED=140°-![]() =
=![]() .
.
∵∠BAC=100°,∠DAC=n,
∴∠BAD=100°+n,
∴∠BAD=2∠CDE.

 名校课堂系列答案
名校课堂系列答案