��Ŀ����
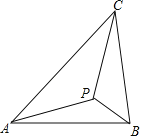
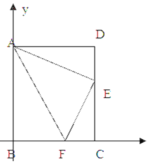
����Ŀ����ͼ������ABC�У�AB=AC=12cm��BC=9cm����DΪAB���е㣮
��1�������P���߶�BC����3����/����ٶ���B��C���˶���ͬʱ��Q���߶�CA����C����A���˶���
������Q���˶��ٶ����P���˶��ٶ���ȣ�������1��ʱ����BPD����CQP�Ƿ�ȫ�ȣ����жϲ�˵�����ɣ�
������Q���˶��ٶ����P���˶��ٶȲ���ȣ�����Q���˶��ٶ�Ϊ����ʱ���ܹ�ʹ��BPD�ա�CPQ��
��2������Q�Ԣڵ��˶��ٶȴӵ�C��������P��ԭ���˶��ٶȴӵ�Bͬʱ����������ʱ������ABC�������˶������ʱ�䣬��P���Q��һ������ABC���������ϻ�������
���𰸡���1�����ǣ�����������![]() ����2��24�룬BC
����2��24�룬BC
��������
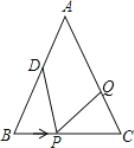
��1���������BP=CQ=3��PC=BD=6��Ȼ����ݵȱ߶ԵȽ���á�B=��C��������SAS����֤����
����ΪVP��VQ������BP��CQ���֡�B=��C��Ҫʹ��BPD���CQPȫ�ȣ�ֻ��BP=CP=4.5������ȫ�ȵó�CQ=BD=6��Ȼ������˶��ٶ�����˶�ʱ�䣬����ʱ���CQ�ij��������Q���˶��ٶȣ�
��2����ΪVQ>VP��ֻ���ǵ�Q�ϵ�P������Q�ȵ�P����AB+AC��·�̣��ݴ��г����̣���������̼������.
���
(1)�١�t=1(��)
��BP=CQ=3(cm)
��AB=12��DΪAB�е�
��BD=6(cm)
�֡�PC=BCBP=93=6(cm)
��PC=BD
��AB=AC
���B=��C
�ڡ�BPD���CQP�У�
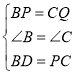
���BPD�ա�CQP(SAS)��
�ڡ�VP��VQ
��BP��CQ
�֡ߡ�B=��C
Ҫʹ��BPD�ա�CPQ��ֻ��BP=CP=4.5(cm)��
�ߡ�BPD�ա�CPQ
��CQ=BD=6(cm)
���P���˶�ʱ��![]() ��
��
��ʱ![]() .
.
(2)��ΪVQ>VP��ֻ���ǵ�Q�ϵ�P������Q�ȵ�P����AB+AC��·�̣�
�辭��x���P��Q��һ���������������4x=3x+2��12��
���x=24(��)
��ʱP�˶���24��3=72(cm)
�֡ߡ�ABC���ܳ�Ϊ33cm��72��33=2��6��
���P��Q��BC������������������24�룬��P���Q��һ����BC����������

 ���Ͱ�ͨ��ĩ���ϵ�д�
���Ͱ�ͨ��ĩ���ϵ�д�