题目内容
【题目】在![]() 中,
中,![]() ,
,![]() ,点
,点![]() 为
为![]() 的中点.
的中点.
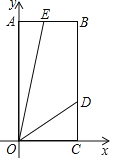
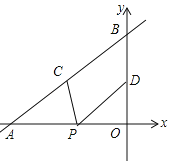
(1)如图;![]() 为线段
为线段![]() 上任意一点,将线段
上任意一点,将线段![]() 绕点
绕点![]() 顺时针方向旋转
顺时针方向旋转![]() 得到线段DF,连结CF,过点
得到线段DF,连结CF,过点![]() 作
作![]() ,交直线
,交直线![]() 于点
于点![]() .
.
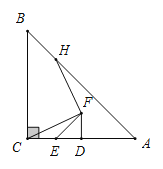
①若![]() ,求
,求![]() 的度数;
的度数;
②判断![]() 与
与![]() 的数量关系并加以证明.
的数量关系并加以证明.
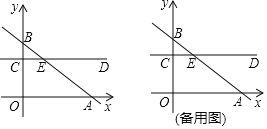
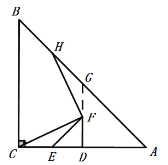
(2)如图,若![]() 为线段
为线段![]() 的延长线上任意一点,(1)中的其他条件不变,你在(1)②中得出的结论是否发生改变,给出证明.
的延长线上任意一点,(1)中的其他条件不变,你在(1)②中得出的结论是否发生改变,给出证明.

【答案】(1)①22.5°;②FH=FC;(2)不变,证明见解析
【解析】
(1)①利用等腰直角三角形斜边等于直角边的![]() 倍,结合已知证得
倍,结合已知证得![]() ,利用三角形外角定理即可求得答案;
,利用三角形外角定理即可求得答案;
②易证得![]() 为等腰直角三角形,由等量代换证得
为等腰直角三角形,由等量代换证得![]() 和
和![]() ,从而证得
,从而证得![]()
![]()
![]() ,即可得到结论;
,即可得到结论;
(2)![]() 和
和![]() 为等腰直角三角形,由等量代换证得
为等腰直角三角形,由等量代换证得![]() 和
和![]() 从而证得
从而证得![]() ,即可得到结论.
,即可得到结论.
(1)①∵![]() 且
且![]()
∴![]() 为等腰直角三角形
为等腰直角三角形
∴![]()
又∵![]()
∴![]()
∴![]()
∵![]()
∴![]()
②延长![]() 交
交![]() 于点
于点![]()
∵![]()
∴![]()
∵![]()
∴![]()
∴![]() 为等腰直角三角形
为等腰直角三角形
∴![]()
∵![]() 是
是![]() 中点
中点
∴![]() 即
即![]()
而ED=FD
∴![]()
又∵![]() 为等腰直角三角形
为等腰直角三角形
∴![]()
∴![]()
∵![]()
∴![]()
在![]() 和
和![]() 中
中
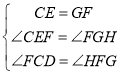
∴![]() (
(![]() )
)
∴![]()
(2)不变.
设![]() 交
交![]() 于点
于点![]()
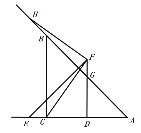
![]() 和
和![]() 为等腰直角三角形
为等腰直角三角形
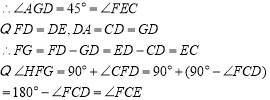
在![]() 和
和![]() 中
中
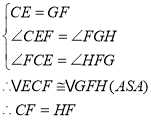

练习册系列答案
 小学能力测试卷系列答案
小学能力测试卷系列答案
相关题目