ΧβΡΩΡΎ»ί
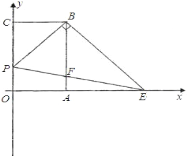
ΓΨΧβΡΩΓΩ»γΆΦΘ§ΤΫΟφ÷±Ϋ«Ήχ±ξœΒ÷–Θ§÷±œΏABΘΚyΘΫkx+3Θ®kΓΌ0Θ©ΫΜx÷α”ΎΒψAΘ®4Θ§0Θ©Θ§ΫΜy÷α’ΐΑκ÷α”ΎΒψBΘ§ΙΐΒψCΘ®0Θ§2Θ©Ήςy÷αΒΡ¥ΙœΏCDΫΜAB”ΎΒψEΘ§ΒψP¥”E≥ωΖΔΘ§―ΊΉ≈…δœΏEDœρ”“‘ΥΕ·Θ§…ηPEΘΫnΘ°
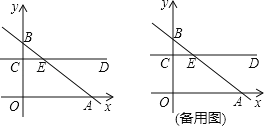
Θ®1Θ©«σ÷±œΏABΒΡ±μ¥ο ΫΘΜ
Θ®2Θ©Β±ΓςABPΈΣΒ»―ϋ»ΐΫ«–Έ ±Θ§«σnΒΡ÷ΒΘΜ
Θ®3Θ©»τ“‘ΒψPΈΣ÷±Ϋ«ΕΞΒψΘ§PBΈΣ÷±Ϋ«±Ώ‘Ύ÷±œΏCDΒΡ…œΖΫΉςΒ»―ϋRtΓςBPMΘ§ ‘Έ ΥφΉ≈ΒψPΒΡ‘ΥΕ·Θ§ΒψM «Ζώ“≤‘Ύ÷±œΏ…œ‘ΥΕ·ΘΩ»γΙϊ‘Ύ÷±œΏ…œ‘ΥΕ·Θ§«σ≥ωΗΟ÷±œΏΒΡΫβΈω ΫΘΜ»γΙϊ≤Μ‘Ύ÷±œΏ…œ‘ΥΕ·Θ§«κΥΒΟςάμ”…Θ°
ΓΨ¥πΑΗΓΩΘ®1Θ©y=©¹![]() x+3ΘΜΘ®2Θ©n=
x+3ΘΜΘ®2Θ©n=![]() Μρ
Μρ![]() +
+![]() Μρ©¹
Μρ©¹![]() +2
+2![]() ΘΜΘ®3Θ©‘Ύ÷±œΏ…œΘ§άμ”…ΦϊΫβΈω
ΘΜΘ®3Θ©‘Ύ÷±œΏ…œΘ§άμ”…ΦϊΫβΈω
ΓΨΫβΈωΓΩ
Θ®1Θ©ΫΪΒψAΒΡΉχ±ξ¥ζ»κ÷±œΏABΘΚy=kx+3≤ΔΫβΒΟΘΚk=©¹![]() Θ§Φ¥Ω…«σΫβΘΜ
Θ§Φ¥Ω…«σΫβΘΜ
Θ®2Θ©Ζ÷AP=BPΓΔAP=ABΓΔAB=BP»ΐ÷÷«ιΩωΘ§Ζ÷±π«σΫβΦ¥Ω…ΘΜ
Θ®3Θ©÷ΛΟςΓςMHPΓ’ΓςPCBΘ®AASΘ©Θ§«σ≥ωΒψMΘ®n+![]() Θ§n+
Θ§n+![]() Θ©Θ§Φ¥Ω…«σΫβΘ°
Θ©Θ§Φ¥Ω…«σΫβΘ°
Θ®1Θ©ΫΪΒψAΒΡΉχ±ξ¥ζ»κ÷±œΏABΘΚy=kx+3≤ΔΫβΒΟΘΚk=©¹![]() Θ§
Θ§
Ι ABΒΡ±μ¥ο ΫΈΣΘΚy=©¹![]() x+3ΘΜ
x+3ΘΜ
Θ®2Θ©Β±y=2 ±Θ§x=![]() Θ§Ι ΒψEΘ®
Θ§Ι ΒψEΘ®![]() Θ§2Θ©Θ§‘ρΒψPΘ®n+
Θ§2Θ©Θ§‘ρΒψPΘ®n+![]() Θ§2Θ©Θ§
Θ§2Θ©Θ§
ΕχΒψAΓΔBΉχ±ξΖ÷±πΈΣΘΚΘ®4Θ§0Θ©ΓΔΘ®0Θ§3Θ©Θ§
‘ρAP2=Θ®![]() +n©¹4Θ©2+4ΘΜBP2=Θ®n+
+n©¹4Θ©2+4ΘΜBP2=Θ®n+![]() Θ©2+1Θ§AB2=25Θ§
Θ©2+1Θ§AB2=25Θ§
Β±AP=BP ±Θ§Θ®![]() +n©¹4Θ©2+4=Θ®n+
+n©¹4Θ©2+4=Θ®n+![]() Θ©2+1Θ§ΫβΒΟΘΚn=
Θ©2+1Θ§ΫβΒΟΘΚn=![]() ΘΜ
ΘΜ
Β±AP=AB ±Θ§Ά§άμΩ…ΒΟΘΚn=![]() Θ®≤ΜΚœΧβ“β÷Β“―…α»ΞΘ©ΘΜ
Θ®≤ΜΚœΧβ“β÷Β“―…α»ΞΘ©ΘΜ
Β±AB=BP ±Θ§Ά§άμΩ…ΒΟΘΚn=©¹![]() +2
+2![]() ΘΜ
ΘΜ
Ι nΘΫ![]() Μρ
Μρ![]() +
+![]() Μρ©¹
Μρ©¹![]() +2
+2![]() ΘΜ
ΘΜ
Θ®3Θ©‘Ύ÷±œΏ…œΘ§άμ”…ΘΚ
»γΆΦΘ§ΙΐΒψMΉςMDΓΆCD”ΎΒψHΘ§
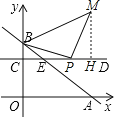
ΓΏΓœBPC+ΓœPBC=90ΓψΘ§ΓœBPC+ΓœMPH=90ΓψΘ§
ΓύΓœCPB=ΓœMPHΘ§BP=PMΘ§ΓœMHP=ΓœPCB=90Γψ
ΓύΓςMHPΓ’ΓςPCBΘ®AASΘ©Θ§
‘ρCP=MH=n+![]() Θ§BC=1=PHΘ§
ȧBC=1=PHȧ
Ι ΒψMΘ®n+![]() Θ§n+
Θ§n+![]() Θ©Θ§
Θ©Θ§
n+![]() +1= n+
+1= n+![]() Θ§
Θ§
Ι ΒψM‘Ύ÷±œΏy=x+1…œΘ°