题目内容
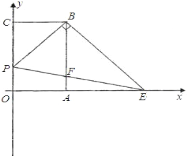
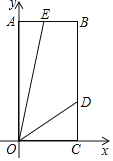
【题目】如图,平面直角坐标系中,长方形OABC,点A,C分别在y轴,x轴的正半轴上,OA=6,OC=3.∠DOE=45°,OD,OE分别交BC,AB于点D,E,且CD=2,则点E坐标为_____.
【答案】(![]() ,6)
,6)
【解析】
如图,过点E作EF⊥OE交OD延长线于点F,过点F作FG⊥AB交AB延长线于点G,作FH⊥BC于H,由“AAS”可证△AEO≌△GEF,可得AE=GF,EG=AO=6,通过证明△ODC∽△FDH,可得![]() ,即可求解.
,即可求解.
如图,过点E作EF⊥OE交OD延长线于点F,过点F作FG⊥AB交AB延长线于点G,作FH⊥BC于H,
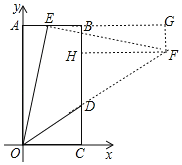
∵∠EOF=45°,EF⊥EO,
∴∠EOF=∠EFO=45°,
∴OE=EF,
∵∠AOE+∠AEO=90°,∠AEO+∠GEF=90°,
∴∠GEF=∠AOE,且∠OAE=∠G=90°,OE=EF,
∴△AEO≌△GEF(AAS)
∴AE=GF,EG=AO=6,
∴BG=EG﹣BE=6﹣(3﹣AE)=3+AE,
∵FH⊥BC,∠G=∠CBG=90°,
∴四边形BGFH是矩形,
∴BH=GF=AE,BG=HF=3+AE,HF∥BG∥OC,
∴HD=BD﹣BH=4﹣AE,
∵HF∥OC,
∴△ODC∽△FDH,
∴![]() ,
,
∴![]()
∴AE=![]() ,
,
∴点E(![]() ,6)
,6)
故答案为:(![]() ,6)
,6)

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目