题目内容
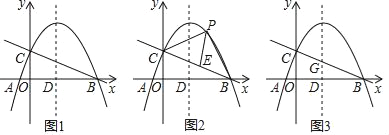
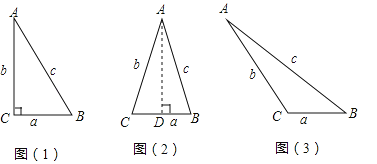
【题目】在△ABC中,BC=a,AC=b,AB=c,若∠C=90°,如图1,则有![]() ;若△ABC为锐角三角形时,小明猜想:
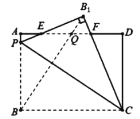
;若△ABC为锐角三角形时,小明猜想:![]() ,理由如下:如图2,过点A作AD⊥CB于点D,设CD=x.在Rt△ADC中,
,理由如下:如图2,过点A作AD⊥CB于点D,设CD=x.在Rt△ADC中,![]() ,在Rt△ADB中,
,在Rt△ADB中,![]() ,∴
,∴![]() .
.
∵a>0,x>0,∴2ax>0,∴![]() ,∴当△ABC为锐角三角形时
,∴当△ABC为锐角三角形时![]() .
.
所以小明的猜想是正确的.
(1)请你猜想,当△ABC为钝角三角形时, ![]() 与
与![]() 的大小关系.
的大小关系.
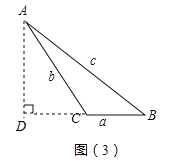
(2)温馨提示:在图3中,作BC边上的高.
(3)证明你猜想的结论是否正确.
【答案】(1)![]() ;(2)作图见解析;(3)正确.
;(2)作图见解析;(3)正确.
【解析】
试题分析:(1)根据题意可猜测:当△ABC为钝角三角形时,![]() 与
与![]() 的大小关系为:
的大小关系为:![]() ;
;
(2)根据题意可作辅助线:过点A作AD⊥BC于点D;
(3)然后设CD=x,分别在Rt△ADC与Rt△ADB中,表示出AD2,即可证得结论.
试题解析:(1)当△ABC为钝角三角形时,![]() 与
与![]() 的大小关系为:
的大小关系为:![]() ;
;
(2)如图3,过点A作AD⊥BC于点D;
(3)证明:如图3,设CD=x.在Rt△ADC中,![]() ,在Rt△ADB中,
,在Rt△ADB中,![]() ,∴
,∴![]() .∵a>0,x>0,∴2ax>0,∴
.∵a>0,x>0,∴2ax>0,∴![]() ,∴当△ABC为钝角三角形时,
,∴当△ABC为钝角三角形时,![]() .
.

练习册系列答案
相关题目