题目内容
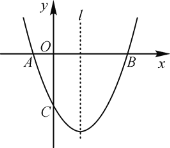
【题目】如图1,在平面直角坐标系中,抛物线y=﹣![]() x2+
x2+![]() x+
x+![]() 与x轴交于A、B两点(点A在点B的左侧),与y轴交于点C,对称轴与x轴交于点D.
与x轴交于A、B两点(点A在点B的左侧),与y轴交于点C,对称轴与x轴交于点D.
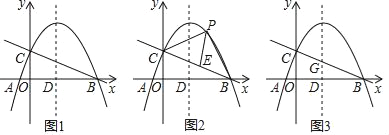
(1)求直线BC的解析式;
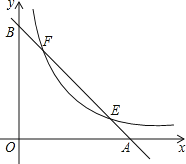
(2)如图2,点P为直线BC上方抛物线上一点,连接PB、PC.当△PBC的面积最大时,在线段BC上找一点E(不与B、C重合),使PE+![]() BE的值最小,求点P的坐标和PE+
BE的值最小,求点P的坐标和PE+![]() BE的最小值;
BE的最小值;
(3)如图3,点G是线段CB的中点,将抛物线y=﹣![]() x2+
x2+![]() x+
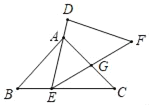
x+![]() 沿x轴正方向平移得到新抛物线y′,y′经过点D,y′的顶点为F.在抛物线y′的对称轴上,是否存在一点Q,使得△FGQ为直角三角形?若存在,直接写出点Q的坐标;若不存在,请说明理由.
沿x轴正方向平移得到新抛物线y′,y′经过点D,y′的顶点为F.在抛物线y′的对称轴上,是否存在一点Q,使得△FGQ为直角三角形?若存在,直接写出点Q的坐标;若不存在,请说明理由.
【答案】(1)直线BC的解析式为y=﹣![]() x+
x+![]() ;(2)P(
;(2)P(![]() ,
,![]() ),PE+
),PE+![]() BE=
BE=![]() ;(3)存在,Q(﹣1,
;(3)存在,Q(﹣1,![]() )或(﹣1,
)或(﹣1,![]() ),理由见解析
),理由见解析
【解析】
(1)根据二次函数的解析式先求出点C、点B的坐标,然后利用待定系数法即可求出直线BC的解析式;
(2)如图2中,过点P作PM⊥x轴于点M,交直线BC于点F,过点E作EN⊥x轴于点N,设P(a,﹣![]() a2+
a2+![]() a+
a+![]() ),则F(a,﹣
),则F(a,﹣![]() a+
a+![]() )则可得 PF=﹣
)则可得 PF=﹣![]() a2+
a2+![]() a,继而得S△PBC=﹣
a,继而得S△PBC=﹣![]() a2+
a2+![]() a,根据二次函数的性质可得当a=
a,根据二次函数的性质可得当a=![]() 时,S△PBC最大,可得点P坐标,由直线BC的解析式为y=﹣
时,S△PBC最大,可得点P坐标,由直线BC的解析式为y=﹣![]() x+
x+![]() 可得∠CBO=30°,继而可得PE+
可得∠CBO=30°,继而可得PE+![]() BE=PE+EN,根据两点之间线段最短和垂线段最短,则当P,E,N三点共线且垂直于x轴时,PE+
BE=PE+EN,根据两点之间线段最短和垂线段最短,则当P,E,N三点共线且垂直于x轴时,PE+![]() BE值最小,据此即可求得答案;
BE值最小,据此即可求得答案;
(3)由题意可得D(1,0),G(![]() ,
,![]() ),继而可得直线DG解析式,根据抛物线y=﹣
),继而可得直线DG解析式,根据抛物线y=﹣![]() x2+
x2+![]() x+
x+![]() =﹣
=﹣![]() (x﹣1)2+
(x﹣1)2+![]() 沿x轴正方向平移得到新抛物线y′,y′经过点D,可得y'═﹣
沿x轴正方向平移得到新抛物线y′,y′经过点D,可得y'═﹣![]() (x+1)2+
(x+1)2+![]() ,从而可得对称轴为x=﹣1,然后分∠QDG=90°或∠QGD=90°,∠GQD=90°三种情况进行讨论即可得.
,从而可得对称轴为x=﹣1,然后分∠QDG=90°或∠QGD=90°,∠GQD=90°三种情况进行讨论即可得.
(1)当x=0时,y=﹣![]() x2+
x2+![]() x+
x+![]() =
=![]() ,
,
∴点C的坐标为(0,![]() );
);
当y=0时,有﹣![]() x2+
x2+![]() x+
x+![]() =0,
=0,
解得:x1=﹣1,x2=3,
∴点B的坐标为(3,0),
设直线BC的解析式为y=kx+b(k≠0),
将B(3,0)、C(0,![]() )代入y=kx+b,得:
)代入y=kx+b,得:
![]() ,解得:
,解得: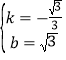 ,
,
∴直线BC的解析式为y=﹣![]() x+
x+![]() ;
;
(2)如图2中,过点P作PM⊥x轴于点M,交直线BC于点F,过点E作EN⊥x轴于点N,
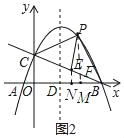
设P(a,﹣![]() a2+
a2+![]() a+
a+![]() ),则F(a,﹣
),则F(a,﹣![]() a+
a+![]() ),
),
∴PF=﹣![]() a2+
a2+![]() a,
a,
∴S△PBC=![]() ×PF×3=﹣
×PF×3=﹣![]() a2+
a2+![]() a,
a,
∴当a=![]() 时,S△PBC最大,
时,S△PBC最大,
∴P(![]() ,
,![]() ),
),
∵直线BC的解析式为y=﹣![]() x+
x+![]() ,
,
∴∠CBO=30°,EN⊥x轴,
∴EN=![]() BE,
BE,
∴PE+![]() BE=PE+EN,
BE=PE+EN,
∴根据两点之间线段最短和垂线段最短,则当P,E,N三点共线且垂直于x轴时,PE+![]() BE值最小,
BE值最小,
∴PE+![]() BE=PE+EN=PN=
BE=PE+EN=PN=![]() ;
;
(3)∵D是对称轴直线x=1与x轴的交点,G是BC的中点,
∴D(1,0),G(![]() ,
,![]() ),
),
∴直线DG解析式y=![]() x﹣
x﹣![]() ,
,
∵抛物线y=﹣![]() x2+
x2+![]() x+
x+![]() =﹣
=﹣![]() (x﹣1)2+
(x﹣1)2+![]() 沿x轴正方向平移得到新抛物线y′,y′经过点D,
沿x轴正方向平移得到新抛物线y′,y′经过点D,
∴y'═﹣![]() (x+1)2+
(x+1)2+![]() ,
,
∴对称轴为x=﹣1,
∵△FGQ为直角三角形,
∴∠QDG=90°或∠QGD=90°,∠GQD=90°(不合题意,舍去),
当∠QDG=90°,设直线QD解析式y=﹣![]() x+b,过D(1,0),
x+b,过D(1,0),
∴0=﹣![]() +b,
+b,
b=![]() ,
,
∴y=﹣![]() x+
x+![]() ,
,
当x=﹣1时,y=![]() ,
,
∴Q(﹣1,![]() ),
),
当∠QGD=90°,则直线QD解析式y=﹣![]() x+
x+![]() ,
,
∴当x=﹣1时,y=![]() ,
,
∴Q(﹣1,![]() ).
).

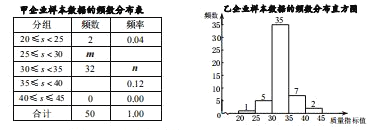
【题目】某地质量监管部门对辖区内的甲、乙两家企业生产的某同类产品进行检查,分别随机抽取了 50 件产品并对某一项关键质量指标做检测,获得了它们的质量指标值 s ,并对样本数据(质量指标值 s )进行了整理、描述和分析.下面给出了部分信息.
a.该质量指标值对应的产品等级如下:
质量指标值 | 20 ≤ s 25 | 25 ≤ s 30 | 30 ≤ s 35 | 35 ≤ s 40 | 40 ≤ s ≤ 45 |
等级 | 次品 | 二等品 | 一等品 | 二等品 | 次品 |
说明:等级是一等品,二等品为质量合格(其中等级是一等品为质量优秀); 等级是次品为质量不合格.
b.甲企业样本数据的频数分布统计表如下(不完整):
c.乙企业样本数据的频数分布直方图如下:
d.两企业样本数据的平均数、中位数、众数、方差如下:
平均数 | 中位数 | 众数 | 方差 | |
甲企业 | 31.92 | 32.5 | 34 | 11.87 |
乙企业 | 31.92 | 31.5 | 31 | 15.34 |
根据以上信息,回答下列问题:
(1) m 的值为 , n 的值为 ;
(2)若从甲企业生产的产品中任取一件,估计该产品质量合格的概率为 ; 若乙企业生产的某批产品共5 万件,估计质量优秀的有 万件;
(3)根据图表数据,你认为 企业生产的产品质量较好,理由为 .(从某个角度说明推断的合理性)